
| Title | The divisor choice in xtgee | |
| Author | David M. Drukker, StataCorp |
Technical Note: This is a technical FAQ. Technical FAQs address specific issues or computational aspects of estimators or other commands. They are typically written for someone who already knows and fully understands the statistics of the command—an expert in the area. All of the materials in the Stata manual, including the Methods and Formulas and sometimes the references, are assumed to be understood.
These FAQs often deal with issues that are not considered or adequately addressed in the literature, and as such we welcome insights from readers or related citations that we may have missed.
The default divisor for computing correlations and standard errors in xtgee is N, the number of observations in the dataset. With this divisor, the estimates are invariant to the scale of the dataset. Scale invariance is an important property. No weights are equivalent to frequency weights of one. If you multiply these weights by a scale factor, you would not want your estimates to change.
In some other packages and in some previous versions of xtgee, the divisor is N − p, where p is the number of covariates in the model. This divisor is used to obtain unbiased estimates. This divisor, however, causes the estimates not to be scale invariant. As N goes to infinity, the difference between the two divisors goes to zero.
In xtgee, if you specify the option nmp, the divisor N − p will be used instead of the default divisor N.
The scaling issue also affects the normalization factor for the robust VCE when family(gaussian) is specified. Historically, xtgee used {(npanels)/(npanels − 1)}{(N − 1)/(N − p)}, where npanels is the number of panels in the dataset and N and p are defined as above. This normalization factor would prevent the VCE from being invariant to the scale of the weights. For this reason, the default normalization factor is now (npanels)/(npanels − 1) instead of {(npanels)/(npanels − 1)} {(N − 1)/(N − p)}. One can use the previous normalization factor by specifying the option rgf.
The divisor used in computing the unstructured and nonstationary correlation matrices for each element in the correlation matrix has changed to the number of panels that have valid observations for the ti and tj defined by that element.
With balanced data, xtgee and SAS version 6.12 Genmod will produce the same results if the correct options are specified. For models with family(Gaussian) and link(identity), the default options for each correlation structure produce matching results. For non-Gaussian models, Stata sets the scale coefficient to 1 by default. In contrast, SAS Genmod defaults to setting the scale parameter to the Pearson chi-squared. One can match the SAS Genmod results with Stata’s xtgee by specifying the scale(x2) option.
For unbalanced data, Stata’s xtgee and SAS version 6.12 Genmod do not produce exactly the same results. Theoretically, GEE estimation with family(gaussian), link(identity), and correlation(independent) should produce the same results as simple linear regression. Stata’s xtgee does reduce to simple OLS under these conditions; however, SAS Genmod does not. Instead of
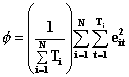
SAS Genmod is using
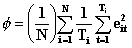
This difference indicates that SAS Genmod forces the panels to have the same weight instead of an implicit weighting determined by length as is done in the first formula.
For more complex correlation structures, it is not possible to back out the specific differences between the packages. Analogous differences in computing the scale parameter and the parameters of the correlation matrix are probably responsible for the differences in the results obtained by the two packages.
To investigate the behavior of Stata’s xtgee, I conducted a Monte Carlo study with 10,000 replications. The data were generated from a process
yit=-1+x1it+2*x2it+3*x3it+4*x4it+eit
where eit is gaussian and autoregressive with a correlation coefficient of .3.
On each of these datasets, I ran
. xtgee y x1 x2 x3 x4, family(gaussian) link(identity) i(id) corr(ar 1)
and saved the relevant information. (The code running these simulations can be obtained by clicking here.)
The following table gives the mean of the estimates that I obtained for the coefficients and the autoregression parameter over the 10,000 runs. The means of the estimates are all within .012 of the true parameter.
Variable | Obs Mean Std. Dev. Min Max
---------+-----------------------------------------------------
x1 | 10000 1.011026 .9790695 -2.778255 4.613505
x2 | 10000 1.993917 .4733509 .3084104 3.762877
x3 | 10000 2.999791 .2484509 2.03008 3.949788
x4 | 10000 3.999901 .2136448 3.205784 4.835913
cons | 10000 -1.005913 .5871637 -3.055032 1.362445
rho | 10000 .2996235 .0167369 .2390387 .3540029
I then checked the p-values that resulted from a hypothesis test against the null that coefficient was its true value. Since there were 10,000 runs, one expects there to be about 500 p-values less than or equal to .05. The following table indicates that this is what I found.
Variable | # of P-Values <=.05
----------|--------------------
x1 | 492
x2 | 489
x3 | 519
x4 | 515
_cons | 475
The results indicate that Stata’s xtgee is performing well on unbalanced data.
To run the simulations first, obtain ar_sim.ado by clicking here. Make sure to save the program as ar_sim.ado. Then within Stata, use the simulate command as follows
. set mem 10m
. simulate ar_sim, reps(10000)
For more information, see [R] simulate. Although exact execution times will differ according to processor and disk drive speeds, running all 10,000 replications takes a long time.