|
This FAQ is for Stata 10 and older versions of Stata.
What does “completely determined” mean in my logistic regression output?
| Title |
|
Interpreting “...completely determined” when running logistic |
| Author |
Willim Sribney, StataCorp
|
| Date |
January 1999; minor revisions May 2005
|
There are two causes for messages like
note: 4 failures and 0 successes completely determined.
after the commands
logistic,
logit, and
probit.
Let us deal with the most unlikely case first:
Case 1: A continuous variable is a great predictor
This case occurs when a continuous variable (or a combination of a
continuous variable with other continuous or dummy variables) is simply a
great predictor of the dependent variable.
Important note: Here there will be no missing standard errors.
If you have a missing standard error in your output, see Case 2
below.
This case is best explained by example. Consider Stata’s
auto.dta with 6 observations removed.
. sysuse auto, clear
(1978 Automobile Data)
. drop if foreign==0 & gear_ratio>3.1
(6 observations deleted)
. logit foreign mpg weight gear_ratio
Iteration 0: log likelihood = -42.806086
Iteration 1: log likelihood = -17.438677
Iteration 2: log likelihood = -11.209232
Iteration 3: log likelihood = -8.2749141
Iteration 4: log likelihood = -7.0018452
Iteration 5: log likelihood = -6.5795946
Iteration 6: log likelihood = -6.4944116
Iteration 7: log likelihood = -6.4875497
Iteration 8: log likelihood = -6.4874814
Iteration 9: log likelihood = -6.4874814
Logistic regression Number of obs = 68
LR chi2(3) = 72.64
Prob > chi2 = 0.0000
Log likelihood = -6.4874814 Pseudo R2 = 0.8484
------------------------------------------------------------------------------
foreign | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
mpg | -.4944907 .2655508 -1.86 0.063 -1.014961 .0259792
weight | -.0060919 .003101 -1.96 0.049 -.0121698 -.000014
gear_ratio | 15.70509 8.166234 1.92 0.054 -.3004359 31.71061
_cons | -21.39527 25.41486 -0.84 0.400 -71.20747 28.41694
------------------------------------------------------------------------------
note: 4 failures and 0 successes completely determined.
A simple plot shows what is going on:
. scatter foreign gear_ratio
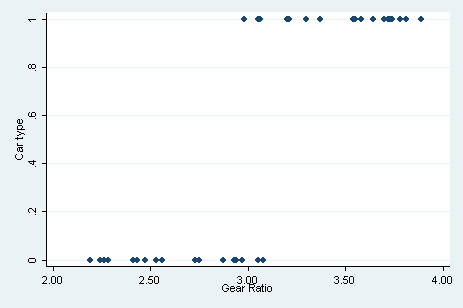
Obviously, gear_ratio is a great predictor of
foreign. It thought that the 4 observations with
the smallest predicted probabilities were essentially predicted perfectly.
. predict p
(option pr assumed; Pr(foreign))
. sort p
. list p in 1/4
+----------+
| p |
|----------|
1. | 1.34e-10 |
2. | 6.26e-09 |
3. | 7.84e-09 |
4. | 1.49e-08 |
+----------+
What to do if this happens
If this happens to you, there is no need to do anything. The model computed
is fine. It is the second case, discussed below, that requires careful
examination.
Case 2: Hidden collinearity
This case occurs when the independent terms are all dummy variables or
continuous variables with multiple values (e.g., age). Here one or more of
the estimated coefficients will have missing standard errors.
Here is an example:
Example 1
. list
+-------------+
| y x1 x2 |
|-------------|
1. | 0 0 0 |
2. | 0 1 0 |
3. | 1 1 0 |
4. | 0 0 1 |
5. | 1 0 1 |
+-------------+
. logit y x1 x2, nolog
Logistic regression Number of obs = 5
LR chi2(2) = 1.18
Prob > chi2 = 0.5530
Log likelihood = -2.7725887 Pseudo R2 = 0.1761
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x1 | 18.26157 2 9.13 0.000 14.34164 22.1815
x2 | 18.26157 . . . . .
_cons | -18.26157 1.414214 -12.91 0.000 -21.03338 -15.48976
------------------------------------------------------------------------------
note: 1 failure and 0 successes completely determined.
. predict p
(option pr assumed; Pr(y))
. sort p
. list
+------------------------+
| y x1 x2 p |
|------------------------|
1. | 0 0 0 1.17e-08 |
2. | 0 1 0 .5 |
3. | 1 1 0 .5 |
4. | 0 0 1 .5 |
5. | 1 0 1 .5 |
+------------------------+
Here the covariate pattern x1 = 0 and x2 = 0 only has y = 0 as an outcome
(and never y = 1). Further, it is possible for the logit model to fit the
outcome for the covariate pattern x1 = 0 and x2 = 0 perfectly.
Example 2
Having a covariate pattern with only one outcome is necessary for this
completely determined situation to occur but not sufficient.
For example, add another observation with a new covariate pattern, and the
completely determined case does not occur.
. list
+-------------+
| y x1 x2 |
|-------------|
1. | 0 0 0 |
2. | 0 1 0 |
3. | 1 1 0 |
4. | 0 0 1 |
5. | 1 0 1 |
|-------------|
6. | 0 1 1 |
+-------------+
. logit y x1 x2
Iteration 0: log likelihood = -3.819085
Logistic regression Number of obs = 6
LR chi2(2) = 0.00
Prob > chi2 = 1.0000
Log likelihood = -3.819085 Pseudo R2 = 0.0000
------------------------------------------------------------------------------
y | Coef. Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
x1 | 0 1.837117 0.00 1.000 -3.600684 3.600684
x2 | 0 1.837117 0.00 1.000 -3.600684 3.600684
_cons | -.6931472 1.732051 -0.40 0.689 -4.087904 2.70161
------------------------------------------------------------------------------
. predict p
(option pr assumed; Pr(y))
. sort p
. list
+------------------------+
| y x1 x2 p |
|------------------------|
1. | 0 0 0 .3333333 |
2. | 0 1 0 .3333333 |
3. | 1 1 0 .3333333 |
4. | 0 0 1 .3333333 |
5. | 1 0 1 .3333333 |
|------------------------|
6. | 0 1 1 .3333333 |
+------------------------+
A technical explanation
Let’s look at the data of example 1 again:
. list
+------------------------+
| y x1 x2 p |
|------------------------|
1. | 0 0 0 1.17e-08 |
2. | 0 1 0 .5 |
3. | 1 1 0 .5 |
4. | 0 0 1 .5 |
5. | 1 0 1 .5 |
+------------------------+
If the observations corresponding to the covariate
pattern with only one outcome (here the first observation)
are dropped, then x1,
x2, and the constant are collinear. This
is what is happening when you get the message ... completely
determined. You have
- A covariate pattern (or patterns) with only one outcome.
- When the observations corresponding to this covariate pattern
are dropped, there is collinearity.
What to do if this happens
First confirm that this is what is happening. (For your data, replace
x1 and x2
with the independent variables of your model.)
- Number covariate patterns:
egen pattern = group(x1 x2)
- Identify pattern with only one outcome:
logit y x1 x2
predict p
summarize p
* the extremes of p will be almost 0 or almost 1
tab pattern if p < 1e-7 // (use a value here slightly bigger than the min)
* or in the above use "if p > 1 - 1e-7" if p is almost 1
list x1 x2 if pattern == XXXX // (use the value here from the tab step)
* the above identifies the covariate pattern
- The covariate pattern that predicts outcome perfectly may be
meaningful to the researcher or may be an anomaly due to having many
variables in the model.
- Now you must get rid of the collinearity:
logit y x1 x2 if pattern ~= XXXX // (use the value here from the tab step)
* note that there is collinearity
*You can omit the variable that logit drops or drop another one.
- Refit the model with the collinearity removed:
logit y x1
You may or may not want to include the covariate pattern that predicts
outcome perfectly. It depends on the answer to (3). If the covariate
pattern that predicts outcome perfectly is meaningful, you may want to
exclude these observations from the model:
logit y x1 if pattern ~= XXXX
Here one would report
- Covariate pattern such and such predicted outcome perfectly
- The best model for the rest of the data is ....
|
