In the spotlight: irt
New to Stata 14 is a suite of commands to fit item response theory (IRT) models. IRT models are used to analyze the relationship between the latent trait of interest and the items intended to measure the trait. Stata’s irt commands provide easy access to some of the commonly used IRT models for binary and polytomous responses, and irtgraph commands can be used to plot characteristic functions and information functions.
To learn more about Stata’s IRT features, refer to the [IRT] Item Response Theory Reference Manual; here I want to go beyond the manual and show you some examples of what you can do with a little bit of Stata code.
The dataset used in the examples contains answers to nine binary items, q1–q9. I do not show much Stata code here; see the accompanying blog entry for details, including replication code.
Example 1
To get started, I want to show you how simple IRT analysis is in Stata.
When I use the nine binary items q1–q9, all I need to type to fit a 1PL model is
. irt 1pl q*
Equivalently, I can use a dash notation or explicitly spell out the variable names:
. irt 1pl q1-q9 . irt 1pl q1 q2 q3 q4 q5 q6 q7 q8 q9
I can also use parenthetical notation:
. irt (1pl q1-q9)
Parenthetical notation is not very useful for a simple IRT model, but it comes in handy when you want to fit a single IRT model to combinations of binary, ordinal, and nominal items:
. irt (1pl q1-q5) (1pl q6-q9) (pcm x1-x10) ...
IRT graphs are equally simple to create in Stata. For example, to plot item characteristic curves (ICCs) for all the items in a model, I type
. irtgraph icc
Yes, that’s it!
Example 2
Sometimes, I want to fit the same IRT model on two different groups and see how the estimated parameters differ between the groups. This exercise can be part of investigating differential item functioning (DIF) or parameter invariance.
I split the data into two groups, fit two separate 2PL models, and create two scatterplots to see how close the parameter estimates for discrimination and difficulty are for the two groups. For simplicity, my group variable is 1 for odd-numbered observations and 0 for even-numbered observations.
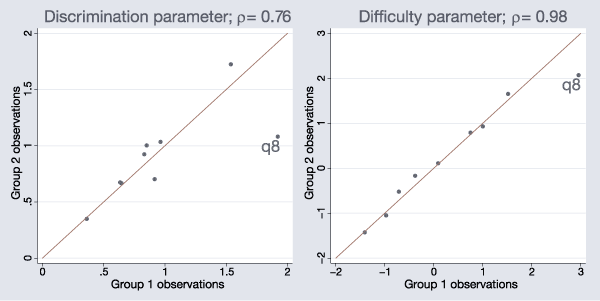
We see that the estimated parameters for item q8 appear to differ between the two groups.
Example 3
Continuing with the example above, I want to show you how to use a likelihood-ratio test to test for item-parameter differences between groups.
Using item q8 as an example, I want to fit one model that constrains item q8 parameters to be the same between the two groups and fit another model that allows these parameters to vary.
The first model is easy. I can fit a 2PL model for the entire dataset, which implicitly constrains the parameters to be equal for both groups. I store the estimates under the name equal.
. quietly irt 2pl q* . estimates store equal
To estimate the second model, I need the following:
. irt (2pl q1-q7 q9) (2pl q8 if odd) (2pl q8 if !odd)
Unfortunately, this is illegal syntax. I can, however, split the item into two new variables where each variable is restricted to the required subsample:
. generate q8_1 = q8 if odd . generate q8_2 = q8 if !odd
I estimate the second IRT model, this time with items q8_1 and q8_2 taking the place of the original q8:
. quietly irt 2pl q1-q7 q8_1 q8_2 q9 . estat report q8_1 q8_2 Two-parameter logistic model Number of obs = 800 Log likelihood = -4116.2064
| Coef. Std. Err. z P>|z| [95% Conf. Interval] | ||
| q8_1 | ||
| Discrim | 1.095867 .2647727 4.14 0.000 .5769218 1.614812 | |
| Diff | -1.886126 .3491548 -5.40 0.000 -2.570457 -1.201795 | |
| q8_2 | ||
| Discrim | 1.93005 .4731355 4.08 0.000 1.002721 2.857378 | |
| Diff | -1.544908 .2011934 -7.68 0.000 -1.93924 -1.150577 | |
Now, I can perform the likelihood-ratio test:
. lrtest equal ., force Likelihood-ratio test LR chi2(2) = 4.53 (Assumption: equal nested in .) Prob > chi2 = 0.1040
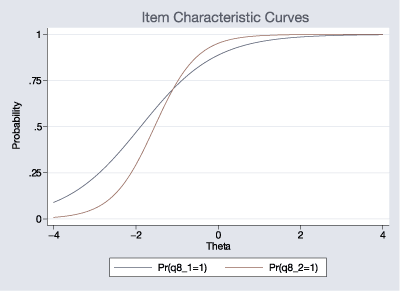
The test suggests the first model is preferable even though the two ICCs clearly differ:
. irtgraph icc q8_1 q8_2, ylabel(0(.25)1)
Summary
IRT models are used to analyze the relationship between the latent trait of interest and the items intended to measure the trait. Stata’s irt commands provide easy access to some of the commonly used IRT models, and irtgraph commands implement the most commonly used IRT plots. With just a few extra steps, you can easily create customized graphs, such as the ones demonstrated above, which incorporate information from separate IRT models. Don’t forget to see the accompanying blog entry that shows the Stata code used in this article.
—Rafal Raciborski
Senior Statistical Developer, StataCorp







