
| Title | Number of observations for subpopulation estimation | |
| Author | Isabel Canette, StataCorp |
Stata estimation commands display the number of observations that participate in the estimation. This number may not be obvious for subpopulation estimation for survey data. I aim to clarify this point in this FAQ, which is organized as follows:
Computing the number of observations for subpopulation estimation can be tricky. For some cases, this number may be different from the number reported in the output for the analogous survey estimation on the whole population. In section 2, I point out some elements we should always account for when counting observations for survey data. To discuss how this number is computed for a subpopulation, I need to introduce some theoretical and practical issues associated with subpopulation estimation; these are addressed in sections 3 and 4. In section 5, I show how to compute the number of observations for a subpopulation estimation on a nonstratified sample where there are missing values in the variables involved in the model. In sections 6 and 7, I address the same information as in section 5 but for stratified designs.
By default, for survey data, the linearized variance estimator is used. To use this estimator, we need all the survey characteristics to be present. If your survey estimation and the analogous nonsurvey estimation are reporting different numbers of observations, this difference is most probably produced by missing values in the survey characteristics. Let’s illustrate with an artificial example based on stage5a.dta.
. webuse stage5a . mean x1 Mean estimation Number of obs = 11,039
| Mean Std. err. [95% conf. interval] | ||
| x1 | -.0072936 .0094905 -.0258967 .0113095 | |
| Linearized | ||
| Mean Std. Err. [95% Conf. Interval] | ||
| x1 | -.0068519 .0043339 -.0174566 .0037527 | |
Here we can see that mean reports 11039 observations. The number of observations reported by svy: mean (11024) does not include the 15 observations that contain missing data for the survey characteristics. If survey characteristics are missing, there is no way to incorporate these observations in our survey computation.
Let’s assume that we want to use highschool.dta to estimate the mean weight for girls. We can use the subpop() option as follows:
. webuse highschool, clear
. quietly svyset county [pw = sampwgt], fpc(ncounties) strata(state)|| school, fpc(nschools)
. svy, subpop(if sex==2): mean weight
(running mean on estimation sample)
Survey: Mean estimation
Number of strata = 50 Number of obs = 4,071
Number of PSUs = 100 Population size = 8,000,000
Subpop. no. obs = 2,133
Subpop. size = 4,151,979
Design df = 50
| Linearized | ||
| Mean Std. Err. [95% Conf. Interval] | ||
| weight | 146.204 .9004157 144.3955 148.0125 | |
The output above will be slightly different from the results we would obtain using the if qualifier:
. svy: mean weight if sex==2
(running mean on estimation sample)
Number of strata = 50 Number of obs = 2,133
Number of PSUs = 100 Population size = 4,151,979
Design df = 50
| Linearized | ||
| Mean Std. Err. [95% Conf. Interval] | ||
| weight | 146.204 .9022106 144.3918 148.0161 | |
Specifying subpop(if sex==2) is not the same as restricting the sample to girls.
If we compute the sum of the sampling weights for all the students in the sample, we will obtain exactly the population size. However, the proportion of girls in the sample depends on the particular sample: the sum of the sampling weights corresponding to all girls in the sample will be an estimate of the number of girls in the population, but it will not necessarily be exactly that number. In other words, if we take a simple random sample from a population that has 50% boys and 50% girls, the sample will have approximately 50% girls but not necessarily exactly that percentage. We need to account for this variation when we compute our standard errors.
If instead of subpop() we used if, we would be pretending that our random sample was designed within the population of girls, and this is not what happened. We designed a sample for the whole population, and we want to use that sample to estimate the mean weight for girls.
The formulas for the estimates of a total and its variance for a simple sampling design with no clusters or stratification are shown in the entry for subpopulation estimation in the [SVY] Survey Data Reference Manual and are transcribed below:
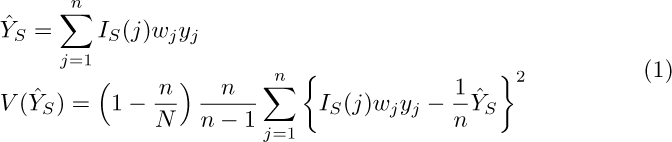
Notice that the whole sample is involved in these computations. Let’s compare these formulas with the ones for the estimates of the totals on the population. From the entry for variance estimation in the [SVY] Survey Data Reference Manual, we can easily deduce that
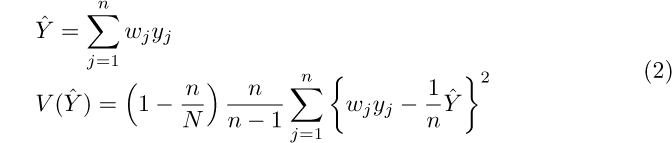
The difference between (1) and (2) is that in (1) survey weights are multiplied by the subpopulation indicator. This is the same as multiplying the weights by zero for the observations that are not in the subpopulation. This assertion also holds with clustered sampling designs when there is no stratification.
In a single stratum design (if the subpopulation is not empty), valid observations outside the subpopulation will be counted in the number of observations, regardless of whether they have missing values in the variables involved in the model.
I will create some examples based on stage5a.dta. I will create a subpopulation variable, S, and I will incorporate some missing values into the variable in the model.
. webuse stage5a, clear . keep in 1/100 (10,939 observations deleted) . quietly svyset [pw=pw] . quietly generate S =cond(_n<51,1,0) . quietly replace x1 = . in 26/100
According to the explanation in section 3, typing
. svy, subpop(S): mean x1
(running mean on estimation sample)
Survey: Mean estimation
Number of strata = 1 Number of obs = 75
Number of PSUs = 75 Population size = 4,015.162
Subpop. no. obs = 25
Subpop. size = 1,520.3704
Design df = 74
| Linearized | ||
| Mean Std. Err. [95% Conf. Interval] | ||
| x1 | -.1399563 .1962026 -.5308986 .250986 | |
is equivalent to multiplying the weight variable by zero for all the observations out of the subpopulation; that is,
. preserve
. replace pw = pw*S
(50 real changes made)
. svy: mean x1
(running mean on estimation sample)
Survey: Mean estimation
Number of strata = 1 Number of obs = 75
Number of PSUs = 75 Population size = 1,520.3704
Design df = 74
| Linearized | ||
| Mean Std. Err. [95% Conf. Interval] | ||
| x1 | -.1399563 .1962026 -.5308986 .250986 | |
We can see that the number of observations reported is different from the number that we would obtain when performing the estimation on the whole population:
. svy: mean x1
(running mean on estimation sample)
Survey: Mean estimation
Number of strata = 1 Number of obs = 25
Number of PSUs = 25 Population size = 1,520.3704
Design df = 24
| Linearized | ||
| Mean Std. Err. [95% Conf. Interval] | ||
| x1 | -.1399563 .198909 -.5504843 .2705717 | |
svy: mean x1 reports that the number of observations is equal to 25, whereas svy, subpop(S): mean x1 reports that the number of observations is equal to 75. Where is this difference coming from?
Let’s have a closer look at the data:
. generate nonmiss = x1 < . . label define nm 0 "missing" 1 "nonmissing" . label values nonmiss nm . tabulate nonmiss S
| S | ||||
| nonmiss | 0 1 | Total | ||
| missing | 50 25 | 75 | ||
| nonmissing | 0 25 | 25 | ||
| Total | 50 50 | 100 | ||
The dataset has 100 observations. Seventy-five observations have missing values for x1, and therefore they are discarded by svy: mean x1. Fifty observations are out of the subpopulation and have a value for x1 of missing. We do not need to know the value of x1 for those observations to perform the subpopulation estimation. Provided that they will be weighted by zero, their actual values would not affect the results. We need only to account for their survey characteristics to incorporate them in our computation of the variance. There is no reason to discard those 50 observations.
By definition of stratified sampling design, samples within different strata are independent. Therefore, if a stratum in the sample does not contain observations for a subpopulation, it does not participate in the corresponding subpopulation estimation. In the following example, the design contains two strata, but only one stratum contains observations from the subpopulation.
. webuse stage5a, clear . quietly keep in 1/200 . *modify the stratification variable . quietly replace strata = cond(_n<101,1,2) . quietly svyset [pw=pw], strata(strata) . *generate a subpopulation variable . quietly generate S = cond(_n<51, 1, 0) . tabulate S strata
| strata | ||||
| S | 1 2 | Total | ||
| 0 | 50 100 | 150 | ||
| 1 | 50 0 | 50 | ||
| Total | 100 100 | 200 | ||
In this dataset, stratum 2 does not contain any elements of the subpopulation. Therefore, only observations in stratum 1 will be counted for the subpopulation estimation. This is also stated at the bottom of the following output:
. svy, subpop(S): mean x1
(running mean on estimation sample)
Number of strata = 1 Number of obs = 100
Number of PSUs = 100 Population size = 5,221.1806
Subpop. no. obs = 50
Subpop. size = 2,726.3889
Design df = 99
| Linearized | ||
| Mean Std. Err. [95% Conf. Interval] | ||
| x1 | .0412889 .1442944 -.2450225 .3276002 | |
Now let’s create a one-stage example that shows how the concepts in the previous sections work together:
. webuse stage5a, clear . set seed 1357 . set sortseed 1 . replace strata = floor((_n-1) /100 ) +1 . svyset [pw=pw], strata(strata) . replace pw = . if runiform()< .1 . replace strata = . if runiform()< .1 . keep in 1/300 . generate S = _n<151 . replace S = 1 in 290/300 . replace x1 = . if uniform()<.2 . replace x1 = . in 290/300 . generate nomiss = x1<.
I will manually count the number of observations for the following estimation:
. svy, subpop(S): mean x1
(running mean on estimation sample)
Survey: Mean estimation
Number of strata = 2 Number of obs = 144
Number of PSUs = 144 Population size = 6,788.3267
Subpop. no. obs = 101
Subpop. size = 5,168.1879
Design df = 142
| Linearized | ||
| Mean Std. Err. [95% Conf. Interval] | ||
| x1 | .0279721 .1013099 -.1722984 .2282426 | |
I will generate a variable named touse that will indicate observations to be used for the subpopulation estimation. This variable will be created in three steps.
Step 1: Rule out observations with missing values for survey characteristics. A quick way to do this is to use svy: mean with a variable equal to 1.
. generate u = 1 . quietly svy: mean u . generate touse = e(sample)
Step 2: Rule out strata without values that are both in the subpopulation and in the regression.
. generate tosum = touse *nomiss *S . bysort strata: egen k = sum(tosum) . replace touse = 0 if k == 0 (79 real changes made)
Step 3: Rule out observations that are in the subpopulation and have missing values in the variables in the model.
. replace touse = 0 if nomiss == 0 & S == 1 (22 real changes made)
Let’s count the observations:
. count if touse 144
This example deals with a one-stage sampling. In a multistage design, you just need to use the stratification for the first stage.