How do I join paired points on a graph?

Note: This FAQ concerns some special graphs of paired observations. If you have multiple measurements per observation and want to generate more standard high-low type charts, these can be created with the connect(||) and connect(II) graph options; see [G] connect.

Suppose you have data reflecting paired measurements, taken before and after an intervention, and you want to draw a graph that joins before and after values, observation by observation.

This can be read in two ways:

Specifically: you have data before and after and want a scatter plot in which before and after are responses on the y-axis and the variable on the x-axis is set to a low or a high constant for before and after, respectively. before should be joined to after for each observation.

        |
        |  *
        |   *
        |    * 
        |  ********
        |      *
        |       *
        |        *
        |         * 
        +-------------
         before after 

More generally: suppose that we have data as variables x1 y1 (= before) x2 y2 (= after). We want to join pairs of points (x1, y1) and (x2, y2). I will show how to do this more general case first.

1. Save the data if important, because the stack command will overwrite it.
2. Generate an identifier if it does not exist:

        . gen id = _n 

3. Stata does not support graphs with more than one variable on the x-axis, so we must stack the data so that two x variables are put in one longer X variable:

        . stack x1 y1 id x2 y2 id, into(X Y ID) clear

4. We have to make sure that the data are in the right order so that only the right pairs of points are joined:

        . egen Xmin = min(X), by(ID)         
        . gsort -Xmin ID X                   
        . gen Y1 = Y if _stack == 1          
        . gen Y2 = Y if _stack == 2          
        . graph Y Y1 Y2 X, c(L..) sy(iop)      

5. The last command ensures that you get distinguishing symbols for y1 and y2. The crucial option is connect(L), which joins points for Y if and only if X is increasing. The gsort command previously put data points in the correct order.

Here is an example of this type of graph. In this case, we are assuming that both X and Y receive some stochastic effect from the regime change.

1. Save the data if important.
2. Generate an identifier if it does not exist.

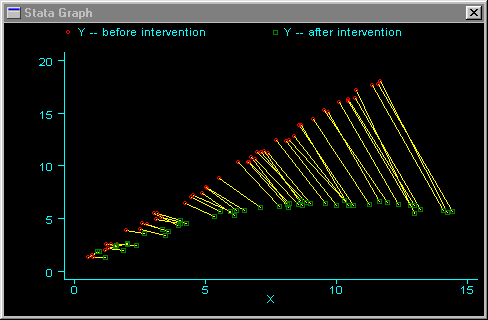
        . gen id = _n

        . stack y1 id y2 id, into(Y ID) clear
        . sort ID _stack
        . graph Y _stack, c(L) 

In this second type of graph, we are not considering the x variable at all. Using the same Y-data from the prior graph, we obtain the following:

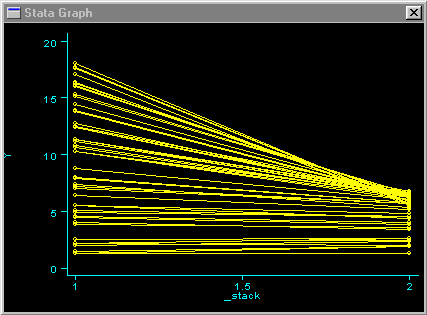
This kind of scatterplot and other plots for this problem are discussed in McNeil (1992).

Reference

McNeil, D. 1992.

On graphing paired data. American Statistician 46: 307–311.