
Thresholds delineate one state from another. There is one effect (one set of coefficients) up to the threshold and another effect (another set of coefficients) beyond it.
Stata's new threshold command fits threshold models.
Threshold models are often applied to time-series data. The threshold can be a time. For example, if you think investment strategies changed as of some unknown date, you can fit a model to obtain an estimate of the date and obtain estimates of the different coefficients before and after it.
Or the threshold can be in terms of another variable. For example, beyond a certain level of inflation, central banks increase interest rates. You can fit a model to obtain an estimate of the threshold and the coefficients on either side of it.
The mayor of a fictional city wants to reduce air pollution caused by the buses the city runs. They have old buses and new buses. The old ones pollute more. They are replacing the old ones with new ones, but it will take awhile. In the meantime, the mayor wonders if pollution could be reduced by running old buses at times of the day when they produce the least amount of pollution.
She has tasked her advisors with finding out. Her advisors model pollutant concentration as a function of the number of old buses, new buses, and cars on the road. They allow the effect of these numbers to vary over time of day. They fit a threshold model. They type
. threshold pollution, threshvar(hour) regionvars(oldbus newbus car)
This command fits a model of pollution on regionvars(), which are
oldbus, newbus, and car.
Variables oldbus, newbus, and car contain
the counts of the vehicles on the road, and variable
pollution contains the measured pollution.
threshvar(hour) is the important part of what they typed. It
instructs threshold to find the hour of
the day when the
coefficients on the regionvars() change.
The data, by the way, are hourly and were collected over the month of January.
The result of fitting the model is
. threshold pollution, threshvar(hour) regionvars(oldbus newbus car)
Threshold regression
Full sample: 01jan2017 00:00:00 - 31jan2017 23:00:00
Number of obs = 744
AIC = -1169.1616
Number of thresholds = 1 BIC = -1132.2652
Threshold variable: hour HQIC = -1154.9393
| Order Threshold SSR |
| 1 12.0000 151.2724 |
| pollution | Coef. Std. Err. z P>|z| [95% Conf. Interval] | |
| Region1 | ||
| oldbus | .0704029 .0093162 7.56 0.000 .0521434 .0886624 | |
| newbus | .0601371 .0086037 6.99 0.000 .0432741 .0770001 | |
| car | .1000345 .0093666 10.68 0.000 .0816763 .1183927 | |
| _cons | 6.995896 .1024878 68.26 0.000 6.795023 7.196768 | |
| Region2 | ||
| oldbus | .2399615 .010146 23.65 0.000 .2200758 .2598473 | |
| newbus | .1446087 .0098378 14.70 0.000 .1253269 .1638904 | |
| car | .1187482 .0095611 12.42 0.000 .1000088 .1374877 | |
| _cons | 9.392377 .1000035 93.92 0.000 9.196374 9.58838 | |
The output appears in three parts: a header, a report on the threshold, and a table of coefficients for each region defined by the threshold.
The threshold is hour = 12.0000, meaning 12 o'clock.
After 12 o'clock, the amount that buses—old and new—pollute increases. Presumably, this is because more of the driving is stop and go. New buses switch their engines off when stopped. Rather interestingly, in region 1 old buses pollute 0.07−0.06 = 0.01 more than new buses. In region 2, they pollute 0.24−0.14 = 0.10 more. This means that swapping an old bus in the morning and a new bus in the afternoon would reduce pollution by 0.10−0.01 = 0.09 while keeping the same number of buses on the street.
The advisors also checked whether there was more than one threshold. They refit the model and told threshold to allow up to four thresholds. They typed
. threshold pollution, regionvars(oldbus newbus car) threshvar(hour)
optthresh(4)
| pollution | Coef. Std. Err. z P>|z| [95% Conf. Interval] | |
| Region1 | ||
| oldbus | .0704029 .0002017 349.06 0.000 .0700076 .0707982 | |
| newbus | .0601371 .0001863 322.85 0.000 .059772 .0605022 | |
| car | .1000345 .0002028 493.31 0.000 .099637 .1004319 | |
| _cons | 6.995896 .0022188 3152.99 0.000 6.991547 7.000245 | |
| Region2 | ||
| oldbus | .2501281 .0004329 577.79 0.000 .2492796 .2509765 | |
| newbus | .1500926 .0004001 375.14 0.000 .1493084 .1508768 | |
| car | .1003077 .0004013 249.96 0.000 .0995212 .1010942 | |
| _cons | 10.49741 .0037666 2787.00 0.000 10.49003 10.5048 | |
| Region3 | ||
| oldbus | .2498727 .0002574 970.78 0.000 .2493683 .2503772 | |
| newbus | .1495873 .0002554 585.65 0.000 .1490867 .1500879 | |
| car | .1002132 .0002433 411.95 0.000 .0997365 .10069 | |
| _cons | 9.002289 .0026688 3373.13 0.000 8.997058 9.00752 | |
threshold reported two thresholds, one at 12:00 p.m. and the other at 3:00 p.m. (15:00). In the scatterplot, we see that the two estimated thresholds correspond with increases in the pollution levels.
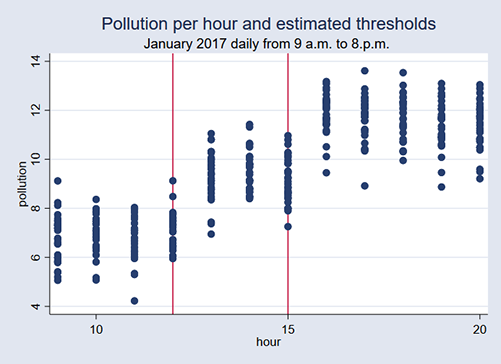
Coefficients changed but the difference in pollution levels between old and new buses is right around 0.10 in both region 2 and region 3. Based on the previous model's results, advisors would have recommended moving old buses from the afternoon to the morning and new buses from the morning to the afternoon. These new results provide no reason for them to change that recommendation.
Learn more about Stata's time-series features.
Read more about threshold and all of Stata's time-series commands in the Stata Time-Series Reference Manual.