What's this about?

Stata now fits nonlinear mixed-effects models, also known as nonlinear multilevel models and nonlinear hierarchical models. These models can be thought of in two ways. You can think of them as nonlinear models containing random effects. Or you can think of them as linear mixed-effects models in which some or all fixed and random effects enter nonlinearly. However you think of them, the overall error distribution is assumed to be Gaussian.

These models are popular because some problems are not, says their science, linear in the parameters. These models are popular in population pharmacokinetics, bioassays, and studies of biological and agricultural growth processes. For example, nonlinear mixed-effects models have been used to model drug absorption in the body, intensity of earthquakes, and growth of plants.

The new estimation command is menl. It implements the popular-in-practice Lindstrom–Bates algorithm, which is based on the linearization of the nonlinear mean function with respect to fixed and random effects. Both maximum likelihood and restricted maximum-likelihood estimation methods are supported.

Let's see it work

Let's look at several examples.

• Random intercepts
• Random coefficients and random-effects covariance structures
• Residual covariance structures: Pharmacokinetic (PK) model
• Nonlinear three-level model: CES production function

Random intercepts

menl is a serious estimator for serious problems. Nonetheless, for pedagogical reasons, we will begin with a silly example. You will remember it.

Suppose we are interested in modeling brain weight growth of unicorns in the land of Zootopia. The graph below shows the brain weight profiles of 20 unicorns over time.

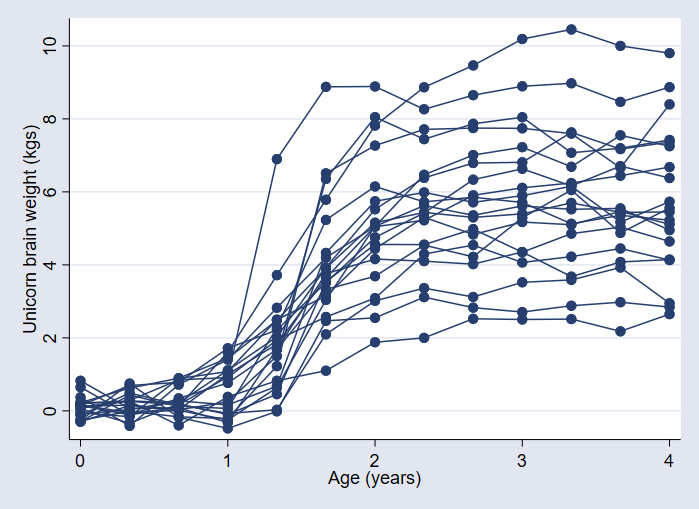
The variability in brain weight measurements between unicorns increases with time.

Based on previous unicorn studies, a model for unicorn brain growth is believed to be

$${\tt weight} = \phi_1/[1+\exp\{-({\tt time}-\phi_2)/\phi_3\}]+\epsilon$$

Parameter \(\phi_1\) represents asymptotic growth—the unicorn's brain weight as time increases to infinity. Parameter \(\phi_2\) is the time at which the brain weight reaches half of \(\phi_1\), and \(\phi_3\) is a scale parameter that determines the growth rate, the rate at which the brain weight approaches the asymptotic weight \(\phi_1\).

We will initially assume that only the asymptotic growth \(\phi_1\) is unicorn specific by including a random intercept \(U_j\) in the equation of \(\phi_1\) for the \(j\)th unicorn:

$$ \eqalign{ \phi_{1} &= \phi_{1j}=\beta_1+ U_{j}\cr \phi_{2} &= \beta_2 \cr \phi_{3} &= \beta_3 } $$

We fit this model using menl as follows:

. menl weight = ({b1}+{U[id]})/(1+exp(-(time-{b2})/{b3}))

Mixed-effects ML nonlinear regression           Number of obs     =        260
Group variable: id                              Number of groups  =         20

						Obs per group:
							      min =         13
							      avg =       13.0
							      max =         13
Linearization log likelihood = -270.54625


      weight 
      Coef.
   Std. Err.
       z
   P>|z|
    [95% Conf. Interval]

         /b1 
   5.722583
    .423781
    13.50
   0.000
     4.891987   6.553178
         /b2 
   1.469935
   .0160542
    91.56
   0.000
     1.438469     1.5014
         /b3 
   .2311064
   .0138384
    16.70
   0.000
     .2039837   .2582292





 Random-effects Parameters 
   Estimate
   Std. Err.
      [95% Conf. Interval]

id: Identity                 

                      var(U)
   3.491344
   1.118415
      1.863457     6.54133

               var(Residual)
   .3355996
   .0306359
      .2806194    .4013517

You can see that the specification to menl looks much like the equation we wrote earlier. Parameters to be estimated are enclosed in curly braces: {b1}, {b2}, and {b3}. By typing {U[id]}, we specified a random intercept for each unicorn, identified by the group variable id.

The above syntax uses what we call a single-equation or single-stage specification. menl also allows multistage or hierarchical specifications in which parameters of interest can be defined at each level of hierarchy as functions of other model parameters and random effects, such as

. menl weight = {phi1:}/(1+exp(-(time-{phi2:})/{phi3:})),
    define(phi1: {b1}+{U1[id]}) 
    define(phi2: {b2}+{U2[id]})
    define(phi3: {b3}+{U3[id]})

Mixed-effects ML nonlinear regression           Number of obs     =        260
Group variable: id                              Number of groups  =         20

						Obs per group:
							      min =         13
							      avg =       13.0
							      max =         13
Linearization log likelihood = -164.64495

    phi1:  {b1}+{U1[id]}
    phi2:  {b2}+{U2[id]}
    phi3:  {b3}+{U3[id]}



      weight 
      Coef.
   Std. Err.
       z
   P>|z|
    [95% Conf. Interval]

         /b1 
   5.800164
   .4243722
    13.67
   0.000
      4.96841   6.631919
         /b2 
    1.50837
   .0278376
    54.18
   0.000
      1.45381   1.562931
         /b3 
   .2304272
   .0312735
     7.37
   0.000
     .1691323   .2917221





 Random-effects Parameters 
   Estimate
   Std. Err.
      [95% Conf. Interval]

id: Independent              

                      var(U1)
   3.542828
   1.125532
      1.900769    6.603452
                      var(U2)
   .0132124
   .0046321
       .006646    .0262667
                      var(U3)
   .0178048
   .0061246
      .0090727    .0349411

               var(Residual)
   .0895668
   .0089351
        .07366    .1089088

This is the same model except that \(\phi_2\) and \(\phi_3\) are also allowed to vary across unicorns using their own sets of random intercepts.

Random coefficients and random-effects covariance structures

Continuing with our unicorn example, we know that boosting brain weight has been an active research area in Zootopia for the past two decades, and scientists believe that consuming rainbow cupcakes right after birth may help attain higher asymptotic growth. Hence, covariate cupcake, which represents the number of rainbow cupcakes consumed right after birth, is added to the equation for \(\phi_{1j}\):

$$\phi_{1j}=\beta_{10}+\beta_{11}\times{\tt cupcake}+U_j$$

We type

. menl weight = {phi1:}/(1+exp(-(time-{b2})/{b3})),
    define(phi1: {b10}+{b11}*cupcake+{U[id]})

Mixed-effects ML nonlinear regression           Number of obs     =        260
Group variable: id                              Number of groups  =         20

						Obs per group:
							      min =         13
							      avg =       13.0
							      max =         13
Linearization log likelihood =  -264.5152

        phi1:  {b10}+{b11}*cupcake+{U[id]}



      weight 
      Coef.
   Std. Err.
       z
   P>|z|
    [95% Conf. Interval]

        /b10 
   4.236238
   .4839165
     8.75
   0.000
     3.287779   5.184697
        /b11 
   .7431848
   .1841062
     4.04
   0.000
     .3823434   1.104026
         /b2 
   1.469951
   .0160856
    91.38
   0.000
     1.438424   1.501478
         /b3 
   .2311114
   .0138654
    16.67
   0.000
     .2039357   .2582872





 Random-effects Parameters 
   Estimate
   Std. Err.
      [95% Conf. Interval]

id: Identity                 

                      var(U)
   1.889632
   .6119155
      1.001692    3.564675

               var(Residual)
   .3355994
   .0306359
      .2806192    .4013515

Consuming rainbow cupcakes after birth indeed leads to higher asymptotic brain growth: /b11 is roughly 0.74 with a 95% CI of [0.38,1.1].

It is bad karma to end a unicorn story without showing how to specify random coefficients or random slopes. Suppose that the equation for \(\phi_{1j}\) is now as follows:

$$\phi_{1j}=\beta_{10}+U_{0j}+(\beta_{11}+U_{1j})\times{\tt cupcake}$$

We incorporated a unicorn-specific random slope for variable cupcake. We also assume that the random effects \(U_{0j}\) and \(U_{1j}\) are correlated. To fit this model, we type

. menl weight = {phi1:}/(1+exp(-(time-{b2})/{b3})),
    define(phi1: {b10}+{U0[id]}+({b11}+{U1[id]})*cupcake)
    covariance(U0 U1, unstructured)

Mixed-effects ML nonlinear regression           Number of obs     =        260
Group variable: id                              Number of groups  =         20

						Obs per group:
                                                              min =         13
                                                              avg =       13.0
                                                              max =         13
Linearization log likelihood = -263.91462

        phi1:  {b10}+{U0[id]}+({b11}+{U1[id]})*cupcake



      weight 
      Coef.
   Std. Err.
       z
   P>|z|
    [95% Conf. Interval]

        /b10 
   4.039338
   .6167933
     6.55
   0.000
    2.830445     5.24823
        /b11 
   .7567096
   .2150858
     3.52
   0.000
     .335149     1.17827
         /b2 
   1.469892
   .0160885
    91.36
   0.000
     1.43836    1.501425
         /b3 
    .231181
    .013868
    16.67
   0.000
    .2040003    .2583618





 Random-effects Parameters 
   Estimate
   Std. Err.
     [95% Conf. Interval]

id: Unstructured              

                    var(U0)
   5.436431
   2.689809
     2.061393    14.33729
                    var(U1)
   .5499744
   .2955551
     .1918265    1.576799
                 cov(U0, U1) 
  -1.675993
   .9083704
    -3.456366    .1043802

               var(Residual)
   .3355991
   .0306359
      .280619    .4013512

In addition to the unstructured covariance, menl supports independent, exchangeable, and identity variance–covariance structures for random effects from the same level of hierarchy.

For more complicated NLME models, specifying expressions containing linear combinations may become tedious. menl offers a convenient shorthand specification to handle linear combinations. For example, the above option define() for phi1 may be replaced with

define(phi1: cupcake U0[id] c.cupcake#U1[id])

Residual covariance structures: Pharmacokinetic (PK) model

menl supports flexible variance–covariance structures to model error heteroskedasticity and its within-group dependence. For example, heteroskedasticity can be modeled as a power function of a covariate or even of predicted mean values, and dependence can be modeled using an autoregressive model of any order.

Consider a PK study in which the drug theophylline was administered orally to 12 subjects with the dosage (mg/kg) given on a per weight basis. Serum concentrations (mg/L) were obtained at 11 time points per subject over 25 hours following administration. The graph below shows the resulting concentration-time profiles for the first four subjects.

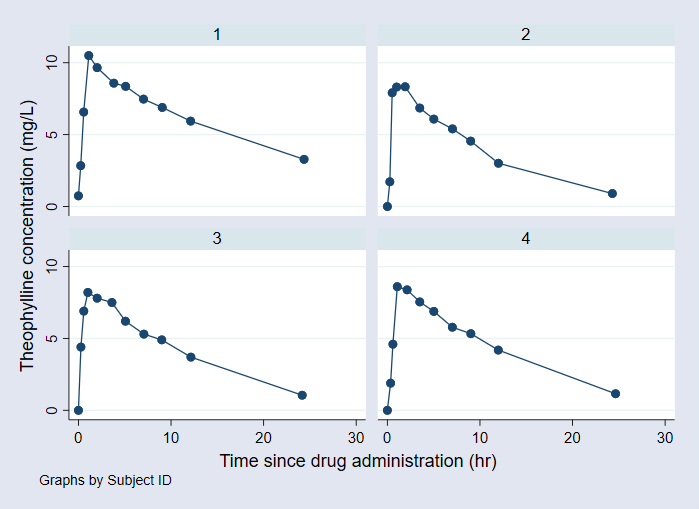
A PK model used to model the above concentration-time profiles is

$$ {\tt conc} = \frac{{\tt dose} \times k_{e} \times k_{a}}{{\rm Cl} \times \left( k_{a} - k_{e} \right)} \left\{ \exp \left( -k_{e} \times {\tt time} \right)-\exp \left( -k_{a} \times {\tt time} \right) \right\} + \epsilon $$

Model parameters are the elimination rate constant \(k_e\), the absorption rate constant \(k_a\), and the clearance \(\rm Cl\). Parameters \(\rm Cl\) and \(k_a\) are allowed to vary across subjects. Because each of the model parameters must be positive to be meaningful, we write

$$ \eqalign{ {\rm Cl} &= {\rm Cl}_j = \exp\left(\beta_0 +U_{0j}\right)\cr k_a &= k_{a_j} = \exp\left (\beta_1 + U_{1j}\right) \cr k_{e} &= \exp\left(\beta_2\right) } $$

It is common for the PK data to exhibit within-subject heterogeneity that increases with the magnitude of the response variable. In this case, the within-subject error variance is often modeled as a power function of the predicted mean. menl provides the resvariance() option for this.

. menl conc = (dose*{ke:}*{ka:}/({cl:}*({ka:}-{ke:})))*(exp(-{ke:}*time)-exp(-{ka:}*time)),
    define(cl: exp({b0}+{U0[subject]}))
    define(ka: exp({b1}+{U1[subject]}))
    define(ke: exp({b2}))
    resvariance(power _yhat)

Mixed-effects ML nonlinear regression           Number of obs     =        132
Group variable: subject                         Number of groups  =         12

                                                Obs per group:
                                                              min =         11
                                                              avg =       11.0
                                                              max =         11
Linearization log likelihood = -167.67964

          cl:  exp({b0}+{U0[subject]})
          ka:  exp({b1}+{U1[subject]})
          ke:  exp({b2})



        conc 
       Coef.
   Std. Err.
       z
   P>|z|
   [95% Conf. Interval]

         /b0 
   -3.227479
   .0598389
   -53.94
   0.000
  -3.344761   -3.110197
         /b1 
     .432931
   .1980835
     2.19
   0.000
   .0446945    .8211674
         /b2 
   -2.453742
   .0514567
   -47.69
   0.000
  -2.554595   -2.352889





 Random-effects Parameters 
   Estimate
   Std. Err.
      [95% Conf. Interval]

id: Independent              

                     var(U0)
   .0288787
   .0127763
      .0121337    .0687323
                     var(U1)
   .4075667
   .1948713
      .1596654    1.040367

Residual variance:           

  Power _yhat                

                      sigma2
   .0976905
   .0833027
       .018366     .519624
                       delta
   .3187133
   .2469511
     -.1653019    .8027285
                       _cons
   .7288982
   .3822952
      .2607507     2.03755

In this example, the 95% CI [-0.2,0.8] for power constant delta contains 0, suggesting that within-subject error variance does not depend on the predicted values.

Nonlinear three-level model: CES production function

Production functions are an important component of macroeconomic models. They tell us how economies use inputs such as labor and capital in the production process. A common example is a constant elasticity of substitution (CES) production function.

The CES function defines how production allocates inputs such as capital and labor. It introduces the constant elasticity of substitution parameter that models the allocation, which makes it a very flexible modeling tool. For instance, CES production functions include Cobb–Douglas, Leontief, and perfect substitutes production functions as special cases.

Let's look at an example.

Suppose that there are five regions, each with seven production firms manufacturing a certain good. Measurements were collected each year over the course of six years. We want to fit the following CES production model,

$$\ln{\rm Q}_{ijt} = \beta_0-(1/\rho)\times\ln\{\delta{\rm K}_{ijt}^{-\rho}+(1-\delta){\rm L}_{ijt}^{-\rho}\}+\epsilon$$

where \(\ln{\rm Q}_{ijt}\), \({\rm K}_{ijt}\), and \({\rm L}_{ijt}\) are the log of output, capital, and labor usage, respectively, for firm \(j\) within region \(i\) at year \(t\). Parameters in this model are log-factor productivity \(\beta_0\) and share \(\delta\), and \(\rho\) is related to the elasticity of substitution.

Parameter \(\rho\) is assumed to be constant in the CES model, but \(\beta_0\) and \(\delta\) may be affected by region-specific and firm-specific effects. For example, here we allow log-factor productivity \(\beta_0\) to be region specific and share parameter \(\delta\) to be firm specific. Because firms are nested within regions, \(\delta\) is technically affected by both firms and regions.

$$ \eqalign{ \beta_{0} &= \beta_{0k}=b_0+ U_{1k}\cr \rho &= b_1 \cr \delta &= \delta_{jk} = b_2 + U_{2jk} } $$

In the above, \(U_{1k}\) and \(U_{2jk}\) are random intercepts at the region and firm-within-region levels.

To fit the above nonlinear three-level model using menl, we type

. menl lnoutput = {b0:}-1/{rho}*ln({delta:}*capital^(-{rho})+(1-{delta:})*labor^(-{rho})),
    define(b0: {b0}+{U1[region]})
    define(delta: {delta}+{U2[region>firm]})

Mixed-effects ML nonlinear regression           Number of obs     =        210



  No. of
      Observations per Group
     Path
  Groups
    Minimum   Average    Maximum

      region 
       5
         42      42.0         42
 region>firm 
      35
          6       6.0          6



Linearization log likelihood = -159.60141

          b0:  {b0}+{U1[region]}
       delta:  {delta}+{U2[region>firm]}



    lnoutput 
       Coef.
   Std. Err.
       z
   P>|z|
   [95% Conf. Interval]

         /b0 
    3.506553
   .1065494
    32.91
   0.000
    3.29772    3.715386
      /delta 
    .5294311
   .0535259
     9.89
   0.000
   .4245222      .63434
        /rho 
    .5355886
   .2306676
     2.32
   0.000
   .0834885    .9876888





 Random-effects Parameters 
   Estimate
   Std. Err.
      [95% Conf. Interval]

region: Identity       

                     var(U1)
   .0267349
   .0210936
      .0056949    .1255072

region>firm: Identity        

                     var(U2)
    .015477
   .0073906
      .0060704    .0394597

               var(Residual)
   .2343921
   .0242961
      .1912982    .2871938

The values of /rho of .54 and /delta of .53 tell us that this economy is allocating capital and labor in roughly equal proportions in the production process.

Regions and firms within regions appear to explain some of the variability in the log-factor productivity parameter and the share parameter, respectively.

We can use nlcom to estimate the elasticity of substitution for the CES production function in this model.

. nlcom (1/(1 + _b[/rho]))

 _nl_1:  1/(1 + _b[/rho])



    lnoutput 
       Coef.
   Std. Err.
       z
   P>|z|
   [95% Conf. Interval]

       _nl_1 
    .6512161
   .0978221
     6.66
   0.000
   .4594884    .8429438

The elasticity of substitution is estimated to be .65 for these data. If instead we used, for example, a Cobb–Douglas production function, we would have incorrectly constrained the elasticity of substitution to be 1.

Tell me more

Learn more about Stata's multilevel mixed-effects models features.

Read more about nonlinear mixed-effects models in the Stata Multilevel Mixed-Effects Reference Manual.