Let's see it work

We will start with that last bullet point, because while the demonstration is simple, if you frequently generate uniform random numbers over a range (or perhaps if you do it infrequently and have a poor memory), this will save you a lot of time.

Let's say we want to generate a random number that is uniformly distributed over an interval, say, (1,7). Back in the old days, we would have to do this with a formula.

Stata 14 introduces two new functions for uniform random numbers: runiform(a,b) and runiformint(a,b). runiform(a,b). Now, all we need to do is type

generate newvar = runiform(1,7)

runiformint(a,b) is used to obtain random integers over the interval [a,b]. It replaces the old method of typing a+int((b-a+1)*runiform()). Results differ slightly because runiformint(a,b) is more precise.

Now, let's take a look at just a couple of possible uses for the statistical distribution functions: simulation and visually comparing different survivor functions.

We want to simulate some survival data and compare our fitted results with the simulated data. This is possible with any of the new random-number generators for survival families, but we are going to demonstrate it for the Weibull(5,3) distribution.

First, we generate 100 observations.

. set obs 100

. set seed 31045

. generate y = rweibull(5,3)

Next, we will fit the model by using streg. We specify coeflegend because we need to know how to refer to the estimated parameters later.

. stset y

     failure event:  (assumed to fail at time=y)
obs. time interval:  (0, y]
 exit on or before:  failure


        100  total observations
          0  exclusions

        100  observations remaining, representing
        100  failures in single-record/single-failure data
    279.762  total analysis time at risk and under observation
                                                at risk from t =         0
                                     earliest observed entry t =         0
                                          last observed exit t =  4.414602


. streg, distribution(weibull) time coeflegend

         failure _d:  1 (meaning all fail)
   analysis time _t:  y

Fitting constant-only model:

(output omitted)


Fitting full model:
Iteration 0:   log likelihood =  10.578599

Weibull regression -- accelerated failure-time form

No. of subjects =          100                  Number of obs    =         100
No. of failures =          100
Time at risk    =   279.761945
                                                LR chi2(0)       =       -0.00
Log likelihood  =    10.578599                  Prob > chi2      =           .


          _t 
 
      Coef.  Legend                                            

       _cons 
   1.110561  _b[_t:_cons]   

       /ln_p 
    1.65018  _b[ln_p:_cons]

           p 
   5.207916                 
         1/p 
   .1920154                 

The Weibull distribution has a shape parameter, a, and a scale parameter, b. We can obtain the estimated values of these parameters by exponentiating streg’s estimates of _cons and ln_p. We use local macros to store these values and the mean of the distribution.

. local a = exp(_b[ln_p:_cons])

. local b = exp(_b[_t:_cons])

. local mean : display %5.2f `b'*exp(lngamma(1+1/`a'))

. display "Fitted Weibull distribution:" 
    _newline  "shape" _skip(10) "scale" _skip(10) "mean" 
    _newline %5.2f `a' _skip(10) %5.2f `b' _skip(10) `mean'

Fitted Weibull distribution:
shape          scale          mean
 5.21           3.04          2.79

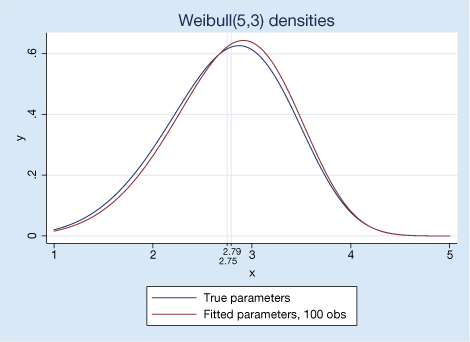
Using these estimated parameters, the true parameters we used to simulate the data, and the new weibullden() function, we can plot our fitted results and the true values with twoway. We also add the true mean 2.75.

We could type

. twoway function y = weibullden(5  ,3  ,x), range(1 5) ||
         function y = weibullden(`a',`b',x), range(1 5)

to graph our true and estimated densities. Or we could add a few graph options and produce

The new distribution functions are also useful for understanding relationships between different statistical families.

We can see how survivor functions for various distributions relate to each other. Recall that the survivor function is 1 minus the cumulative distribution function, S(t) = 1 - F(t).

We plot the survivor function that corresponds to our Weibull(5,3). We add a Weibull(3,3) and Weibull(1,3). To obtain the CDF of the Weibull distribution, we use weibull(a,b). We are also going to plot an exponential(3) with a thin line. You will see that it falls entirely over the Weibull(1,3) because the Weibull(1,b) is equal to the exponential(b). We use exponential(b) to get the CDF of the exponential distribution. Again, subtracting it from one to obtain the corresponding survivor function.

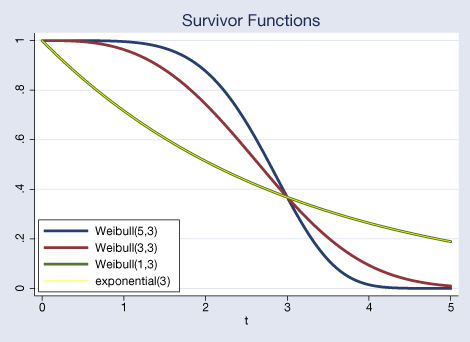
Here is what we typed to obtain that graph.

twoway function w = 1-weibull(5,3,x),   range(0 5) lwidth(thick) ||
       function y = 1-weibull(3,3,x),   range(0 5) lwidth(thick) ||
       function y = 1-weibull(1,3,x),   range(0 5) lwidth(thick) ||
       function y = 1-exponential(3,x), range(0 5) lwidth(thin) color(yellow)
       legend( label(1 "Weibull(5,3)")
               label(2 "Weibull(3,3)")
               label(3 "Weibull(1,3)")
               label(4 "exponential(3)")
               cols(1) ring(0) position(7))
       xtitle("t")
       title(Survivor Functions)

The first four lines use the distribution functions; the rest is just about getting the graph to look the way we wanted.

Tell me more

To find out more about all of Stata’s random-number and statistical distribution functions, see the new 157-page Stata Functions Reference Manual. You can find tips for working with the functions, means and variances of different distributions, and more.