In the spotlight: Bayesian “random-effects” models
Stata 14 introduced bayesmh for fitting Bayesian models. You can choose from one of many built-in models or write your own. See Bayesian analysis and Programming your own Bayesian models for details.
In this article, we show you how to use bayesmh to fit a Bayesian “random-effects” model. We write “random effects” in quotes because all effects (parameters) are considered random within the Bayesian framework. These models are typically referred to as Bayesian multilevel or Bayesian hierarchical models.
We revisit, using the Bayesian approach, the random-effects meta-analysis model described in example 6 of [ME] me. The term “meta-analysis” refers to a statistical analysis that involves summarizing results from similar but independent studies.
We consider data from Turner et al. (2000) that contain estimates of treatment effects expressed as log odds-ratios (lnOR) and their respective variances (var) from nine clinical trials that examined the effect of taking diuretics during pregnancy on the risk of preeclampsia. Negative lnOR values indicate that taking diuretics lowers the risk of preeclampsia. The model can be written as
$$ \begin{eqnarray} {\rm y_{i}} \sim {\rm N}(\mu_{i}), \sigma_{i}^{2} (1)\\ {\rm \mu_{i}} \sim {\rm N}(\theta, \tau^{2}) \end{eqnarray} $$where \(\mu_{i}\) is the mean treatment effect of each trial, \(\theta\) is an overall mean, \(\sigma_{i}^{2}\) is the variance of the observed treatment effect and is considered fixed, and \(\tau^{2}\) is the between-trial variance. \(\theta\) and \(\tau^{2}\) are parameters of interest—\(\tau^{2}\) close to 0 would suggest homogeneity across studies in log odds-ratio estimates.
In example 6 of [ME] me, we fit this random-effects model using meglm and obtain the estimates of \(\theta\) and \(\tau^{2}\) of −0.52 and 0.24 with their respective 95% confidence intervals of [−0.92, −0.11] and [0.048, 1.19].
For our Bayesian analysis, we need to additionally specify priors for \(\theta\) and \(\tau^{2}\) in model (1). Notice that the random-effects model (1) already assumed a normal prior for each individual trial effect \(\mu_{i}\). We consider fairly noninformative normal and inverse gamma prior distributions for the parameters \(\theta\) and \(\tau^{2}\).
$$ \begin{eqnarray} \theta \sim {\rm Normal}(0,10000) (2) \\ \tau^{2} \sim {\rm IG}(0.0001, 0.0001) \end{eqnarray} $$To fit model (1)–(2) using bayesmh, we type
. fvset base none trial
. bayesmh lnOR i.trial, noconstant likelihood(normal(var))
prior({lnOR:i.trial}, normal({theta},{tau2}))
prior({theta}, normal(0,10000))
prior({tau2}, igamma(0.0001,0.0001))
block({lnOR:i.trial}, split) block({theta}, gibbs)
block({tau2}, gibbs) dots
The first four lines of the bayesmh specification are the straightforward model specification. The last two lines improve the efficiency of the sampler—a step that is crucial when fitting high-dimensional hierarchical models such as random-effects models. We sample all parameters separately by placing them in individual blocks and specifying option split for levels of trial, and we also request Gibbs sampling for \(\theta\) and \(\tau^{2}\).
Here is the output:
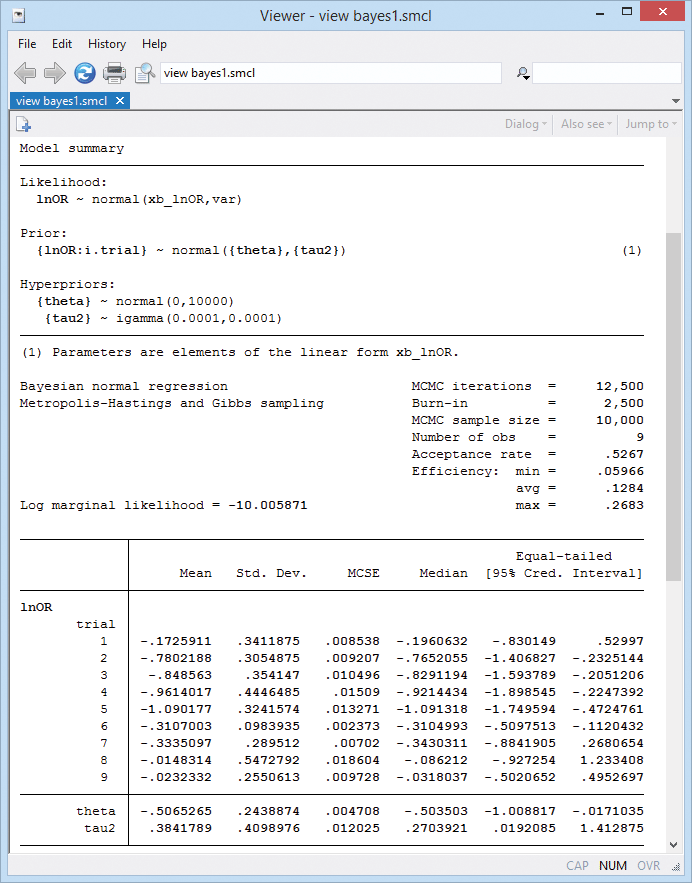
Because we used noninformative priors, our Bayesian results are similar to the frequentist results from example 6. For example, the posterior mean estimate of the overall mean \(\theta\) is −0.51 with a 95% credible interval of [−1.01, −0.017] that represents the ranges to which \(\theta\) belongs with a probability of 0.95.
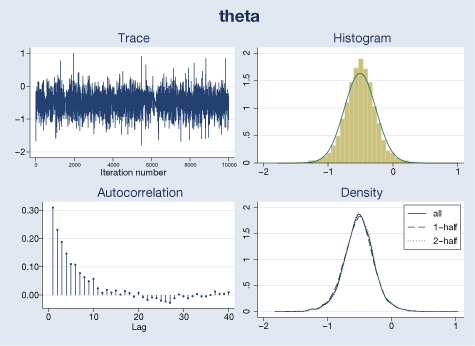
We use bayesgraph to evaluate MCMC convergence visually. For example, here are diagnostics for \(\theta\) and \(\tau^{2}\):
. bayesgraph diagnostics {theta}, histopts(normal)
. bayesgraph diagnostics {tau2}
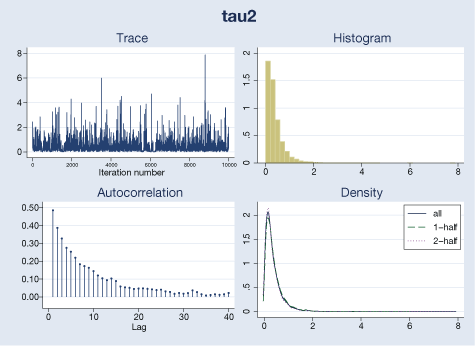
Our visual diagnostics raise no concern for these parameters. We can also check MCMC convergence for trial-specific \(\mu_{i}\)’s by typing
. bayesgraph diagnostics {lnOR:i.trial}
(output omitted)
We can test whether taking diuretics reduces the risk of preeclampsia overall by computing the probability that \(\theta\) is negative.
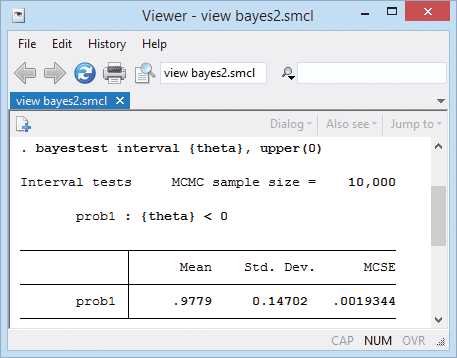
That probability is 0.98.
If desired, we can also compute an estimate of the overall odds ratio.
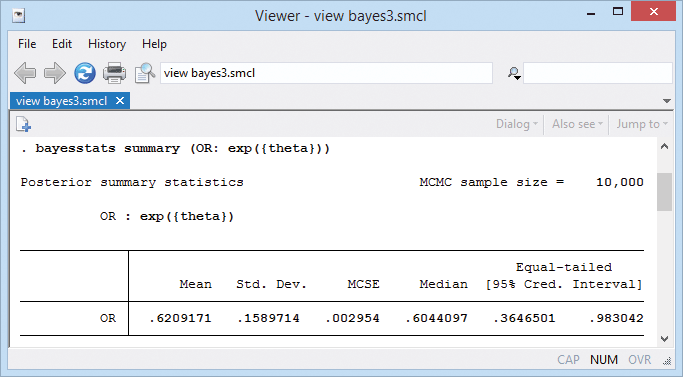
A neat feature of our Bayesian analysis is that we can explore the distributions of the estimated parameters. For example, we can look at distributions of effects from individual trials.
. bayesgraph histogram {lnOR:i.trial},
byparm(legend(off) noxrescale noyrescale
title(Posterior distributions of trial effects))
normal xline(-0.51)
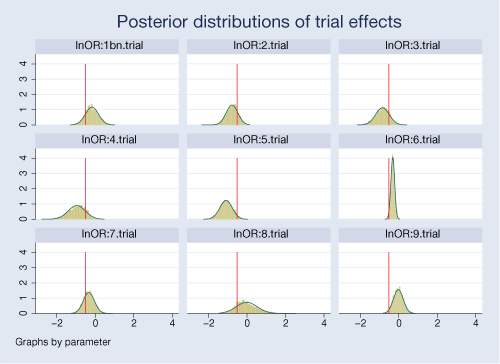
The posterior distributions are fairly normal for most trials. Posteriors for some trials are more closely centered on the overall mean of −0.51, particularly for trials 2 and 7.
There is a noticeable variability in the estimated treatment effects between trials. Trials 6 and 9 are more precise compared with other trials.
We can also test for an effect in each trial. We can estimate a probability that an effect is negative (meaning diuretics work) for each trial. For example,
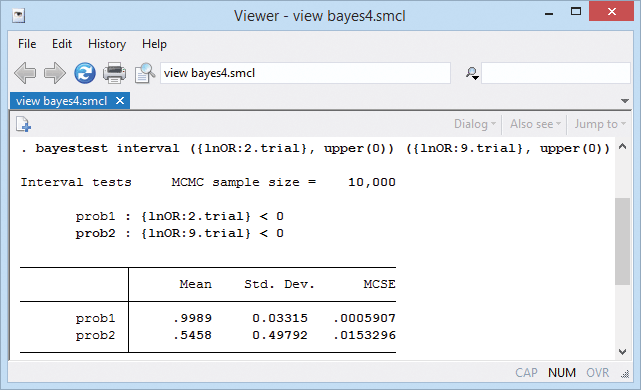
The probability of a negative treatment effect is almost 1 for trial 2 and only about 0.55 for trial 9.
Reference
Turner, R. M., R. Z. Omar, M. Yang, H. Goldstein, and S. G. Thompson. 2000. A multilevel model framework for meta-analysis of clinical trials with binary outcomes. Statistics in Medicine 19: 3417–3432.
— Yulia Marchenko
Director of Biostatistics, StataCorp
— Nikolay Balov
Senior Statistician and Software Developer, StataCorp







