In the spotlight: Meet Stata's new xtmlogit command
Okay, so that title is a bit unfair. We added xtologit and xtoprobit, but the truth is, there is no xtmlogit command. The good news is that you can still fit multinomial logit models to panel data.
If you are like me, you love Stata’s intuitive panel commands. I’m new to StataCorp, and before I got here, I thought panel-data analysis meant I needed a command that started with xt. It turns out that Stata is far more flexible than I knew, and that flexibility comes from a command I never really paid much attention to—gsem. Don’t let the name fool you. It’s still intuitive. Really.
Suppose that I want to analyze the probability of three work-related outcomes for women: employed, unemployed, and not participating in the labor force. I have data on 4,685 women along with some covariates that I think might influence their outcomes.
| varname | Description |
| idcode | individual identifier |
| workstat | status (1=employed, 2=unemployed, 3=out of labor force) |
| age | age in years |
| race | race (1=white, 2=black, 3=other) |
| student | indicator for being a student in the current period |
| msp | indicator for married, spouse present |
Knowing what I know about the xt syntax, I imagine this should work:
xtmlogit workstat age i.race i.student i.msp, re
But what would re mean here? Should Stata assume I want one random effect for each level of workstat or one random effect overall? If I have multiple random effects, should they be independent or should they be correlated?
The intuition for setting up the gsem syntax is that I get to tell Stata exactly what I want. Because I’m fitting a multinomial model, I will omit employed as the base category and use factor-variable notation to specify a separate equation for the other outcomes (for example, 2.workstat means unemployed). I tell Stata that the outcome is a function of the covariates with <-varlist. I want one latent variable that varies at the individual level, which I call RI#[idcode], to capture the random effect for outcome #.
gsem (2.workstat <- age i.race i.student i.msp RI2[idcode])
(3.workstat <- age i.race i.student i.msp RI3[idcode]), mlogit
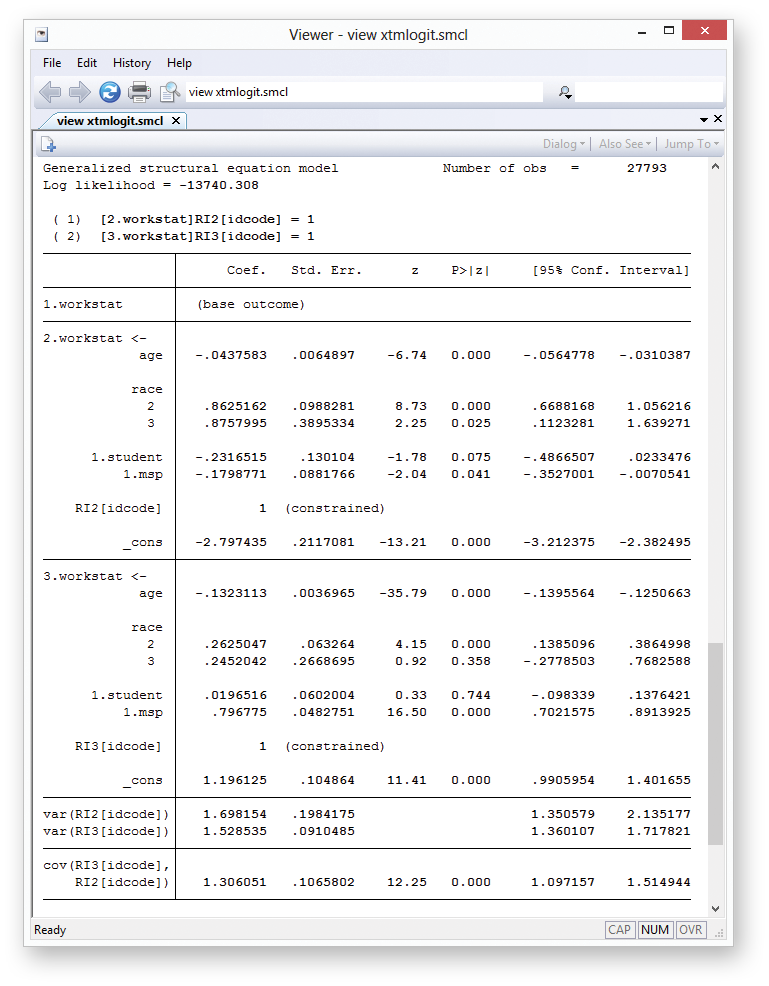
Suppose I am interested in how marital status affects work status. The section for 2.workstat shows a significant negative coefficient for msp, so I conclude that married women have a lower probability of being unemployed relative to being employed. Similarly, married women appear to have a higher probability of being out of the labor force. But that’s just mlogit stuff. If you’re reading this, you probably are more interested in what is different.
The var(RI2[idcode]) and var(RI3[idcode]) terms give the variances of the random effects. In practical terms, these are the variances of the idiosyncratic individual effects. I’m used to reporting random effects in terms of standard deviations. Each of these variance estimates is stored in e(b), so I can see my usual standard deviations this way:
. display sqrt(_b[var(RI2[idcode]):_cons]) 1.3031322
Just beneath that, gsem reports the covariance of my two random terms. The covariance is significant, so I conclude there is an underlying correlation between the two random intercepts.
Now, before you rush out and try this, there are a few caveats. Behind the scenes, Stata is doing a lot of work for you. Every random effect has to be numerically integrated out, and that is time intensive. All the usual rules about time increasing with respect to the number of random effects apply. However, now the number of random effects increases with the number of equations.
This little model took about five minutes to fit, equivalent to the time spent for a trip to the breakroom for coffee. But, if I had added several more outcomes or random coefficients … Let’s just say it’s always nice to take a vacation.
You can see more examples of what gsem is capable of in the [SEM] Structural Equation Modeling Reference Manual. A couple of my other personal favorites are the Heckman selection model and endogenous treatment effects.
—Rebecca Pope
Health Econometrician







