
| Speakers: Patrick Royston, Royal Postgraduate Medical School, and Peter Sasieni, Imperial Cancer Research Fund |
The Cox regression model attempts to quantify the relative hazard of an
event, say death, at varying times after some time origin, such as diagnosis
or initiation of treatment. The data consist of survival times, some of
which are censored if the study ended before an event was observed for every
patient, a censoring indicator variable which is 1 for events and 0 for
censored observations, and usually 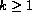 covariates
covariates
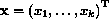 . The hazard
. The hazard 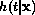 of
death at time t, given the values of the covariates, is represented as
proportional to a baseline hazard function
of
death at time t, given the values of the covariates, is represented as
proportional to a baseline hazard function 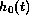 :
:
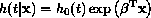
where 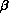 is a vector of regression
coefficients. In the estimation of the parameters,
is a vector of regression
coefficients. In the estimation of the parameters,
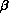 , the baseline hazard function does
not need to be explicitly estimated. This flexibility is perhaps the
strongest feature of the Cox model.
, the baseline hazard function does
not need to be explicitly estimated. This flexibility is perhaps the
strongest feature of the Cox model.
In most medical papers, the authors take the proportional hazards (PH) assumption for granted and make no attempt to check that it has not been violated in their study data. However, it is a strong assumption indeed. Suppose there was a hypothetical treatment which was quite effective in reducing the death rate from some condition during the first year after diagnosis, but whose effectiveness wore off rapidly after that, as the disease process reasserted itself. PH dictates that the treatment effect is constant on the relative hazard scale, so the estimated regression coefficient for treatment from the Cox model will actually represent some kind of time-averaged treatment effect. The important fact that the treatment effect is transient is undetectable within the standard Cox framework.
One approach to detecting non-PH is to extend the Cox model as follows:
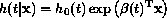
Now 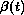 is a function of follow-up
time, thus allowing transient and other time-related covariate effects to be
represented in an intuitive way. There are different ways of gaining an
impression of the nature of
is a function of follow-up
time, thus allowing transient and other time-related covariate effects to be
represented in an intuitive way. There are different ways of gaining an
impression of the nature of 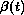 . Two
ways are described here. See Valsecchi et al. (1996) for further details and
examples. The first way is to impose a `window' on the data and estimate
. Two
ways are described here. See Valsecchi et al. (1996) for further details and
examples. The first way is to impose a `window' on the data and estimate
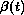 locally within the window
according to a standard Cox model. The window is then shifted and the
process is repeated. It is convenient to define each window as containing a
fixed number of events (deaths), such as 10 × k. The local
estimates of the
locally within the window
according to a standard Cox model. The window is then shifted and the
process is repeated. It is convenient to define each window as containing a
fixed number of events (deaths), such as 10 × k. The local
estimates of the 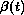 and 95%
confidence intervals, derived as ± 2 times the standard error, are then
plotted against the central time point of each window to give an impression
of the functional form. This approach is implemented in the ado-files
stbtcalc and stbtplot. The second way is through quantities
known as Schoenfeld residuals. The technical details are given by Gramsch
and Therneau (1994) and are not required here. Again a local estimate of
and 95%
confidence intervals, derived as ± 2 times the standard error, are then
plotted against the central time point of each window to give an impression
of the functional form. This approach is implemented in the ado-files
stbtcalc and stbtplot. The second way is through quantities
known as Schoenfeld residuals. The technical details are given by Gramsch
and Therneau (1994) and are not required here. Again a local estimate of
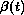 is obtained, but this time it is
essential to apply a smoother to get an impression of the functional form.
We use running (Sasieni 1995; Sasieni & Royston 1998). The
technique is implemented in the ado-files stgtcalc and
stgtplot. Alternatively, a more restricted smoother such as
fracpoly could be applied. Use of fracpoly (or other
parametric models, such as regression splines) has added value in that it
allows us to define, albeit heuristically, significance tests of non-PH.
is obtained, but this time it is
essential to apply a smoother to get an impression of the functional form.
We use running (Sasieni 1995; Sasieni & Royston 1998). The
technique is implemented in the ado-files stgtcalc and
stgtplot. Alternatively, a more restricted smoother such as
fracpoly could be applied. Use of fracpoly (or other
parametric models, such as regression splines) has added value in that it
allows us to define, albeit heuristically, significance tests of non-PH.
Having identified that non-PH is present, the next step may be to try to
model 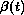 parametrically. It
requires the dataset to be expanded in a particular way, and a Cox
regression with time-varying covariates must be estimated. We won't go into
this here.
parametrically. It
requires the dataset to be expanded in a particular way, and a Cox
regression with time-varying covariates must be estimated. We won't go into
this here.
In the talk, we will give a computer demonstration of the use of the new ado-files in detecting non-proportional hazards in a clinical trial dataset. Some details are given in the next section.
Myelomatosis is a cancer of the bone marrow which affects the immune system.
One of the effects of the disease is the secretion by cancer cells of the
protein 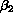 -microglobulin (B2). A
high serum concentration of B2 indicates advanced disease and is associated
with a poor prognosis. The British Medical Research Council has carried out
several controlled clinical trials of treatments for myelomatosis. We
analyze data from the fourth and fifth trials (MacLennan et al. 1988). A
total of 1087 patients were entered, of whom 571 had died by 913 days (about
2.5 years) after randomization, the latest time with complete follow up on
all patients. We use Cox regression to analyze the relation between the B2
concentration at randomization and the log relative hazard of death.
-microglobulin (B2). A
high serum concentration of B2 indicates advanced disease and is associated
with a poor prognosis. The British Medical Research Council has carried out
several controlled clinical trials of treatments for myelomatosis. We
analyze data from the fourth and fifth trials (MacLennan et al. 1988). A
total of 1087 patients were entered, of whom 571 had died by 913 days (about
2.5 years) after randomization, the latest time with complete follow up on
all patients. We use Cox regression to analyze the relation between the B2
concentration at randomization and the log relative hazard of death.
Preliminary analysis reveals k = 4 covariates that are significant
(P < 0.01) predictors of the hazard of death in a multivariable
model. Although treatment effects were significant, the treatments in trials
4 and 5 were different and for simplicity we don't consider them here. The
covariates are the patient's age
(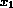 ), and the blood concentrations of
), and the blood concentrations of
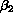 -microglobulin (sb2,
-microglobulin (sb2,
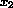 ), hemoglobin (hb,
), hemoglobin (hb,
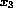 ) and calcium
(
) and calcium
(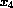 ). The following table shows the
results of analysis using stcox.
). The following table shows the
results of analysis using stcox.
. stset time cens
data set name: myel45.dta
id: -- (meaning each record a unique subject)
entry time: -- (meaning all entered at time 0)
exit time: time
failure/censor: cens
. stcox c2 age sb2 hb calcium
failure time: time
failure/censor: cens
Iteration 0: Log Likelihood = -5353.41
[iteration log omitted]
Cox regression -- entry time 0
No. of subjects = 1050 Log likelihood = -5282.3789
No. of failures = 854 chi2(4) = 142.06
Time at risk = 2659.268992 Prob > chi2 = 0.0000
------------------------------------------------------------------------------
time |
cens | Haz. Ratio Std. Err. z P>|z| [95% Conf. Interval]
---------+--------------------------------------------------------------------
sb2 | 1.028496 .003653 7.911 0.000 1.021361 1.03568
hb | .9932634 .0015708 -4.274 0.000 .9901894 .9963469
calcium | 1.363158 .1127263 3.746 0.000 1.159194 1.60301
age | 1.014327 .004299 3.356 0.001 1.005936 1.022788
------------------------------------------------------------------------------
All the chosen covariates have effects significant at the 0.1% level. Figure 1 shows the graphical output from the stbtplot command, created using the following commands:
. stbtcalc c2 sb2 hb calcium age
. stbtplot sb2 hb calcium age, xlabel(0,1,2,3,4,5,6,7) ylabel ci border
We have omitted results for c2 from the plot to improve legibility. Although there is some noise in each plot, the effect on the hazard is fairly stable over time. The effects of sb2, hb, age and calcium appear time-varying, the least so for calcium. The effect of sb2 seems to reach a peak after about 3–6 months and dwindle thereafter.
Figure 2 shows the graphical output from the stgtplot command, created using the following commands:
. stset time cens
. stcox c2 age sb2 hb calcium
. stgtcalc
. stgtplot sb2 hb calcium age, xlabel(0,1,2,3,4,5,6,7) ylabel ci border
Notice that you must call stcox before stgtcalc, because
stgtcalc (unlike stbtcalc) is a post-estimation command. The
plots provide an estimate of 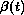 up
to nearly 7 years of follow up—in Figure 1,
up
to nearly 7 years of follow up—in Figure 1,
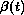 is estimated only up to t
= 5 years. Although the smoothing has not removed all the noise, the
impression again is that all the effects are time-varying. Qualitatively,
the two sets of plots agree quite well, though the effect size generally
seems larger with the stbtcalc approach. When in doubt we should
probably trust the results from stbtcalc more than those from
stgtcalc, since the stbtcalc estimation method is direct and
should not produce much bias.
is estimated only up to t
= 5 years. Although the smoothing has not removed all the noise, the
impression again is that all the effects are time-varying. Qualitatively,
the two sets of plots agree quite well, though the effect size generally
seems larger with the stbtcalc approach. When in doubt we should
probably trust the results from stbtcalc more than those from
stgtcalc, since the stbtcalc estimation method is direct and
should not produce much bias.
We can confirm the subjective impressions from Figure 2 parametrically by
fitting first degree fractional polynomials to estimate
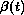 from the Grambsch–Therneau
(GT) residuals and applying a hypothesis test of no effect. The GT residuals
are quietly created by stgtcalc as new variables whose names begin
with the prefix GT. For example, the GT residuals for sb2 are
stored in GTsb2. We would enter
from the Grambsch–Therneau
(GT) residuals and applying a hypothesis test of no effect. The GT residuals
are quietly created by stgtcalc as new variables whose names begin
with the prefix GT. For example, the GT residuals for sb2 are
stored in GTsb2. We would enter
. fracpoly regress GTsb2 time, degree(1) compare
The results show that there is a nonlinear effect of time on GTsb2, since the deviance difference between the first degree fractional polynomial model and the null model is 23.18. The deviance difference is significant at P < 0.001 when compared with chi-squared on 2 df. The first degree fractional polynomial, which has estimated power 0.5, fits significantly better than a straight line (P = 0.023). The same technique applied to age, hb and calcium gives P values of 0.037, 0.45 and 0.13, showing significant non-proportional effects of age but not of hemoglobin or calcium.