1 item has been added to your cart.
| Speaker: Andy Sloggett, London School of Hygiene and Tropical Medicine |
The concept of net mortality is one widely used in cancer epidemiology, although it could certainly be used for other diseases too.
For a cancer patient risk of death can be represented by the following equation:
actual risk of death = underlying risk + cancer risk
If the prevalence of the cancer under study is low then the underlying risk for a cancer patient can be approximated as the all-cause, age/sex-specific death rate. The "cancer risk" is additional risk or net risk due to the fact that the patient has cancer. This additional risk will vary by time since diagnosis.
Net mortality is a useful measure because it allows one to calculate relative survival, which is survival rates excluding causes of death not due to cancer. Relative survival is more useful for comparative purposes as it is a "purer" measure than crude survival. When cancer is rapidly fatal or when it occurs at young ages then crude and relative survival are very similar. However for cancers which occur in the elderly, and for which survival is good, without the use of relative survival it is difficult to get a clear idea of survival from the cancer because there is high "background" mortality polluting the crude estimates. Note that if the cause of death is known then non-cancer deaths could be censored and relative survival calculated this way. However cause of death is not always reliable and it is also difficult to estimate the extent to which the cancer has affected the given cause of death. For these reasons the given cause of death is often ignored and relative survival is commonly used for comparative studies in cancer epidemiology.
But the calculation of net mortality and relative survival has not been particularly convenient because software has invariably been stand-alone, fussy about data format, rather brittle in operation, subject to limitations on number of records etc. Today we present a new Stata command stnet which calculates net mortality rate and relative survival for survival data. It is very fast and can handle large datasets very easily.
The stnet command was written by Michael Hills, Adrian Mander, Bianca de Stavola and Andy Sloggett for use in a cancer survival project at the London School of Hygiene & Tropical Medicine. The project is a collaboration with the Cancer Research Campaign and the Office for National Statistics.
The methodology is that of Jacques Esteve, formerly of IARC, France (Esteve et al. 1990). It is a maximum-likelihood method and calculates net mortality for predefined intervals, assuming the hazard to remain constant across the defined interval. It is beneficial therefore to define small time intervals for periods during which the hazard may be expected to be changing (e.g. first few years post-diagnosis). Crude survival is calculated by normal actuarial methods and the net mortality rate used to correct the cumulative crude survival to produce relative survival.
Using Esteve's procedure person–time in the defined intervals is aggregated and after this only individuals who die in an interval are used in the determination. Other records are dropped. Individual records of those dying have the age, sex, covariate-specific single-year death rate attached to them. Individuals are grouped into the interval in which they die and the net mortality estimated from the risk set for the interval. It can be shown in practice that this method amounts to subtracting expected deaths in the interval from the observed deaths and estimating net mortality from residual deaths.
The log likelihood of the sample is a function of net mortality
(
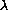) and can be represented as
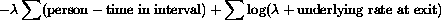
for any one interval.
The result is a net mortality rate for each specified interval. In our work we have usually specified 10 or 17 intervals across 10 years of follow-up. Intervals are not required to be of equal width. Convergence for all intervals is usually achieved in about 12 iterations.
With sparse data non-convergence for one or two intervals can occur. To minimize this we have incorporated a grouping routine which checks for non-convergence and where found groups that interval with an adjacent one. Such grouping is not usually necessary for large datasets if intervals are sensibly chosen. With sparse data grouping becomes more important and complicated routines are necessary to avoid reckless grouping.
Data should be in the form of individual records, similar in layout to that necessary for Cox regression. The stnet command follows the convention of the Stata st commands. The data must be declared st using variables giving the time or age at beginning and end of follow-up, plus an indicator of dead or censored. Example:
stset ageout dead, t0(agediag)
where ageout is age at death or censor, dead is the dead/censored indicator, and agediag is age at entry - usually age at diagnosis of cancer.
A typical command line following stset declaration may be
stnet if sex==1& region==5, br(0[.5]5[1]10) using(ratefile)
mergeby(period sex region age)
where br gives directions on how time intervals post-diagnosis are to be constructed using identifies a file of age- (and covariate- if required) specific death rates, by single year of age (the rates are commonly all-cause rates and provide the "underlying" death rates) and mergeby gives the sort order for merging the rates with the observations. Maximum number of iterations, precision level, starting value for net mortality, and display options can all be set.
Typical output would be
Count of cases
489
NUMBER OF NON-CONVERGENCES DETECTED = 2 :REGROUPING
NUMBER OF NON-CONVERGENCES DETECTED = 1 :REGROUPING
Table of crude and relative survival probabilities
(expressed as percentages with 95% confidence intervals)
left right deaths NetR Crude Cr_lo Cr_up RelR Re_lo Re_up B
0.00 0.50 127 0.5736 73.00 68.77 76.77 75.07 70.69 78.89 .
0.50 1.00 36 0.1703 65.68 61.24 69.74 68.94 64.27 73.13 1
1.00 1.50 23 0.1209 61.05 56.54 65.24 64.90 60.09 69.28 .
1.50 2.00 21 0.1127 56.80 52.26 61.07 61.34 56.43 65.88 .
2.00 2.50 15 0.0671 53.78 49.24 58.10 59.32 54.31 63.97 .
2.50 3.00 11 0.0464 51.55 47.01 55.88 57.96 52.89 62.68 .
3.00 3.50 8 0.0414 49.94 45.42 54.28 56.77 51.66 61.55 .
3.50 4.00 7 0.0169 48.52 44.02 52.88 56.29 51.12 61.14 .
4.00 5.00 10 0.0052 46.52 42.04 50.87 56.00 50.74 60.93 1
5.00 6.00 5 0.0012 45.47 41.00 49.82 55.94 50.61 60.92 .
6.00 7.00 10 0.0278 43.17 38.71 47.54 54.40 48.98 59.50 .
7.00 8.00 8 0.0191 41.20 36.76 45.58 53.37 47.79 58.63 .
8.00 10.00 8 -0.0035 39.00 34.56 43.42 53.37 47.58 58.82 1
Sum of absolute values of first derivatives 2.558e-13
Number of iterations 12
The above output for a dataset of this size would typically take about 4 seconds to produce.
Left and right define the time interval following diagnosis—in this case in years. NetR, Crude, RelR are net mortality rate, cumulative crude survival, and cumulative relative survival respectively.
