3rd UK User Group meeting: Panel Data estimators
James W. Hardin
London Users Group meeting
6 June 1997
Outline
- Panel data
- Estimators
- Identifiability issues
- Monte Carlo Simulation
- Summary
References
1991
J.M. Neuhaus, J.D. Kalbfleisch, and W.W. Hauck
A Comparison of Cluster-Specific and Population Averaged Approaches
for Analyzing Correlated Binary Data
International Statistical Review 59, 25-35.
Comparison of PA and SS models. Authors present two approaches to
comparing these models. Good in combination with the
Zeger/Liang/Albert paper.
References
1996
J.F. Pendergast, S.J. Gange, M.A. Newton, M.J. Lindstrom,
M. Palta, and M.R. Fisher
A Survey of Methods for Analyzing Clustered Binary Response Data
International Statistical Review 64, 89-118.
Survey paper with canonical list of proposed methods. Includes nice
exposition on comparing the methods and a very good long reference
list.
References
1992
J.M. Neuhaus
Statistical methods for longitudinal and clustered designs
with binary responses
Statistical Methods in Medical Research 1, 249-273.
Survey paper which covers not only the PA and SS models, but also
covers the transitional models, response conditional models, and some
hybrid models. This paper also presents a data analysis example from
a longitudinal study of AIDS behaviors among men in San Francisco
which I will use in order to present the types of hypotheses addressed
by the various panel estimators.
References
1988
G. Chamberlain
Analysis of Covariance with Qualitative Data
Review of Economic Studies 225-238.
Comparison of fixed (including conditional) effects and random
effects (focusing on PA models).
References
1988
S.L. Zeger, K.-Y. Liang, and P.S. Albert
Models for Longitudinal Data: A Generalized Estimating
Equation Approach
Biometrics 44, 1049-1060.
Comparison of SS and PA models for longitudinal data. An alternative
comparison here from the presentation in the
Neuhaus paper.
References
1986
K.-Y. Liang and S.L. Zeger
Longitudinal data analysis using generalized linear models
Biometrika 73, 13-22.
This paper was the introduction of the GEE PA model that is in Stata
(xtgee).
Panel Data
In a panel dataset, we have observations for our dependent variable
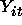such that the observations with common value for i are believed to be
correlated. The i subscript is sometimes referred to as the
individual, panel, subject, cluster, or group. The t subscript
denotes the observation for the particular panel. There are
observations in the general unbalanced case. The t subscript is
called the replication, time, or repeated measure.
Various authors refer to longitudinal data, cross sectional
data, panel
data, and cross-sectional time-series.
Estimators
There are two sources of variability from which we might build an
estimator. There is the variability within (fixed effects) a cluster
and there is the variability between the clusters.
Fixed Effects Estimators
To model fixed effects, one transforms the estimating equation
in order to get rid of the fixed effects.
Random Effects Estimators
There are two obvious ways to approach building a random effects
estimator. One may first assume that:
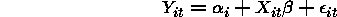
where 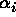 is a random value from some distribution F.
Alternatively, one may assume that
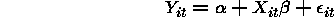
and impose some restrictions on the covariance of 
Random Effects Estimators
In more general terms we can write the model in terms of link
and variance functions as
where 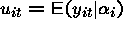 or we may assume that
with
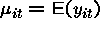 we have
Random Effects Estimators
When are the two approaches the same?
They are the same if all of the 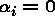 or when the link function
h is the identity. This is because
while 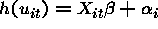 , it is not in general true
that the same link function will have the property
 .
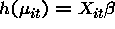Note that the two approaches are the same for linear regression
which uses the identity link. They are not the same for logistic
or probit models that we examine later.
Random Effects Estimators (logit)
The two approaches for logit are
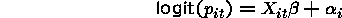
or alternatively, we may look at
along with appropriate assumptions on the covariance of the
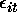 terms (nuisance parameters) and
where we assume that  .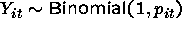
Multilevel models
There are also hybrid models that will estimate the probability
that Y=1 averaged over the observations with the same
covariate patterns. One method for doing this is Goldstein's
multilevel models. These models at their simplest level are
random effects models, but allow the researcher more
flexibility in modeling the outcome.
Other Models
There are also other types of models one can use for analyzing the
panel data. The first is called the transitional model and
models the probability distribution of the outcome at time t,
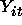as a function of the covariates at time t,  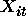, and
the individual’s outcome history  .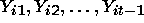
Another model is called the response conditional model which
accomodates correlation by modelling the response probability for
each individual in the panel as a function of covariates for that
individual and the responses for all individuals in that cluster.
Problems with SS Models
- Problems fitting cluster level variables
- Must have more than one observation per panel
Problems with PA Models
- Ignores information leading to coefficient attenuation
Comparison of SS and PA coefficients
Imagine a study where the dependent variable is whether a student performs
acceptably on a standardized test. There are several students under the
direction of each teacher in the study. One of the covariates is whether
the student’s instructor assigns to the individual student Stata in the
classroom for teaching purposes.
Usually, one would consider that the instructor would either use Stata or
not use it in teaching all of the teacher's students. However, imagine that
an instructor is free to assign Stata to some of the students in the
classroom but not to all of the students. So, the use of Stata is not a
cluster level variable.
Interpretation of the coefficient for the SS model
The SS model now allows direct observation and estimation of the average log
odds ratio effect of the change in using Stata to teach upon exam
performance. Mathematically, we collapse across students after we take the
difference in log odds at time points where the instructor did and did not
use Stata in the classroom. The coefficient then represents the common log
odds ratio for passing the exam of the Stata effect across students.
Interpretation of the coefficient for the PA model
The PA coefficient, mathematically, first averages to find the mean risk and
then computes the log odds. The PA model ignores the fact that the effect
of the change in using Stata for an instructor had been measured, and
persist in estimating only the odds ratio between Stata and non-Stata
instructors. Instructors who changed would appear in both groups.
Now imagine, that there really are not any instructors that assign Stata to
a subset of the class so that Stata use is really a cluster level variable.
One cannot directly observe a change in utilizing Stata. The PA model
measures the log odds ratio between the two groups of instructors, whereas
the SS model is supposed to report the effect of the change in the
instructor's usage of Stata. However, no such change was measured, so the
interpretation is entirely model-based as it is a type of extrapolation with
no data to check the validity of the extrapolation. Note that the
conditional likelihood approach for this same model won't allow estimation
of the Stata effect.
Problems with Conditional models
- Can not fit cluster level variables
- Need to check for cluster level collinearity in each cluster
Note that for the logit estimator, the unconditional
fixed-effects
estimator is inconsistent, but the conditional
estimator is consistent.
Let
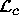 denote the conditional log-likelihood below.
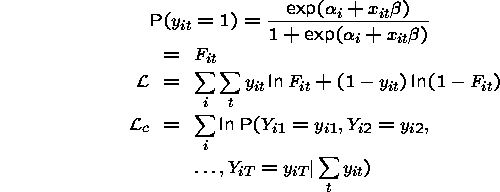
So, the conditional likelihood is conditioned on the number of ones in the
set (panel). Consider an example where there are a large number of panels
each with two time period observations. The unconditional likelihood is
given by
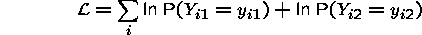
The observations are independent so that the likelihood
function is the
product of the probabilities (we show above the log-likelihood). Note that
for each pair of observations, we have the possibilities
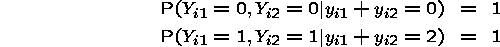
The ith term of 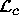for either of these outcomes is just 1. The
log of that is zero, so that either of these outcomes contribute nothing to
the log-likelihood.
Now, suppose that 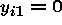 and 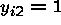 so that
we have
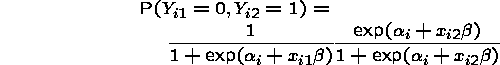
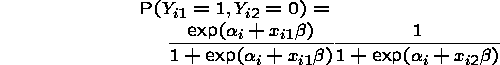
which gives that
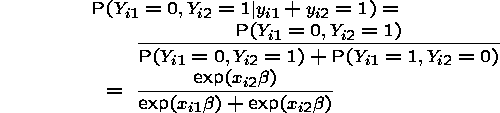
which is free of  .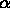
Monte Carlo Simulations
There are two simulations that we ran both generating SS random effects data.
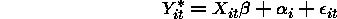
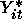 is an unobserved latent variable.
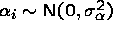 is the random effect.
 is the error term.
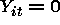 if 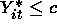 where c is some cutoff value.
Estimators
- Probit
- Probit with robust standard errors
- Maximum likelihood SS random effects probit
- GEE PA probit (exchangeable correlation)
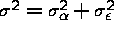
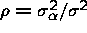
- GEE PA probit (exchangeable correlation) with robust standard errors
Other Estimators
Simulation 1
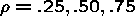
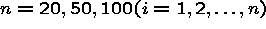
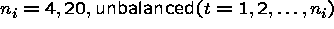
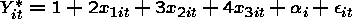
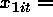 constant within panel (cluster level variable).
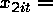 constant across panels (within time)
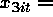 random within and across panels.
r = 1000 is the number of simulations for a given model.
Simulation 2
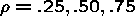
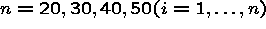
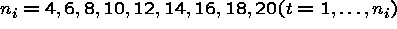
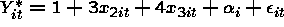
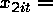constant across panels (within time)
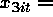random within and across panels.
r = 500 is the number of simulations for a given model.
The main differences for the second simulation were the removal
of the cluster level variable and the focus on smaller datasets.
Random Effects Likelihood
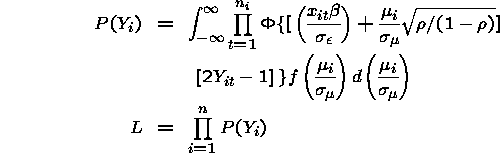
Problems with SS Random Effects Probit
- Problems fitting cluster level variables
- Numeric problems with quadrature
Simulation Results
Probit
- Coverage probability below nominal level.
- Derived test statistics not normally distributed even at very
large sample sizes. As cluster size grows or as
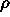 becomes
larger, the estimated standard errors are too small.
Simulation Results
Probit
The probit estimator differed little from the SS-RE model in terms
of RMSE:
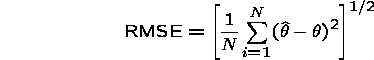
However, misleading results will result if one uses the reported
standard errors in hypothesis tests.
Simulation Results
Probit with robust standard errors
- Coverage probability near nominal level.
- Derived test statistics normally distributed when overall
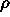sample sizes are larger than 1000 and is small.
Simulation Results
SS Random Effects Probit
- Very good for small samples with low correlation
 .
- Numeric problems with the quadrature calculations
when either
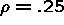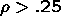 or 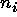becomes large (more than 10).
Simulation Results
SS Random Effects Probit
The major computational problem with the SS Random Effects Probit model is
the need to evaluate the integral using quadrature. It is for these numeric
reasons that this estimator did not perform better. However, it dominated
the other estimators for small values of
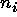and
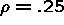. One gains substantial improvement by increasing the
number of Hermite points to about 8 to 10, but not much improvement after
that. Guilkey and Murphy found it necessary to increase this to 16 for
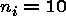 and
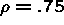 to obtain good performance.
Simulation Results
SS Random Effects Probit
For Simulation 1, where for the cluster level variable, the
SS RE Probit estimator had lower than nominal coverage and
a much larger standard error than the PA Estimator. When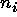
was small (4), the coverage was close to nominal though the
RMSE was larger than for the population averaged approach.
Estimated standard errors are too small when 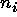or 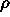get
large due to numerical problems of estimating the integral (not
because the model is faulty).
Simulation Results
PA Random Effects Probit
- Coverage probability near nominal level only for
.
- Derived test statistics normally distributed when overall
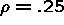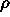sample sizes are larger than 1000 and is small.
- Coefficient estimates smaller than SS model.
Simulation Results
PA Random Effects Probit
Coefficients were smaller than for the SS model as theory dictates.
The standard errors were too small, but coverage is close to nominal
level for small cluster size even when 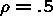 , but not close
to nominal coverage when .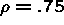
Simulation Results
PA Random Effects Probit with robust standard errors
- Coverage probability near nominal when n>30.
- Derived test statistics normally distributed when overall
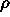sample sizes are larger than 1000 and is small.
Simulation Results
PA Random Effects Probit with robust standard errors
Coefficients were smaller than for the SS model as theory dictates.
The standard errors are of correct size and the coverage is close
to nominal size for all sample sizes and values of
.
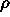Summary
Difference in PA and SS models
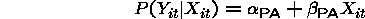
with appropriate assumptions concerning the covariance of
.
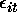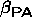 measures the change in proportion with Y=1 for a unit
increase in X. Does not take advantage of repeated measurements on each
study subject and the fact that the effects of the covariate changes within
subjects on the response are directly observable. This model is most
appropriate for cluster level variables.
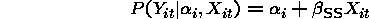
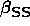 measures the change in probability of response with
covariate X for individuals in each of the underlying risk groups described
by 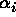. Not appropriate for cluster level variables since this effect
is not directly observable.
Problems with Conditional models
- Can not fit cluster level variables
- Need to check for cluster level collinearity in
each cluster
|
