Home  /  Products  /  Features  /  SEM

<-  See Stata's other features

What is SEM?

View the complete list of SEM features

SEM stands for structural equation modeling. SEM is a notation for specifying structural equations, a way of thinking about them, and methods for estimating their parameters.

SEM encompasses a broad array of models from linear regression to measurement models to simultaneous equations, including along the way confirmatory factor analysis (CFA), correlated uniqueness models, latent growth models, and multiple indicators and multiple causes (MIMIC).

Stata’s sem fits linear SEMs, and its features are described below. gsem provides extensions to linear SEMs that allow for generalized-linear models and multilevel models.

Features

  • Use GUI or command language to specify model.

  • Standardized and unstandardized results.

  • Direct and indirect effects.

  • Goodness-of-fit statistics.

  • Tests for omitted paths and tests of model simplification including modification indices, score tests, and Wald tests.

  • Predicted values and factor scores.

  • Linear and nonlinear (1) tests of estimated parameters and (2) combinations of estimated parameters with CIs.

  • Estimation across groups is as easy as adding group(sex) to the command. Test for group invariance. Easily add or relax constraints across groups.

  • SEMs may be fitted using raw or summary statistics data.

  • Maximum likelihood (ML) and asymptotic distribution free (ADF) estimation. ADF is also known as generalized method of moments (GMM). Missing at random (MAR) data supported via FIML.

  • Robust estimate of standard errors and standard errors for clustered samples available.

  • Support for survey data including sampling weights, stratification and poststratification, and clustered sampling at one or more levels.

SEM Builder or commands, it’s your choice

Enter your model graphically,

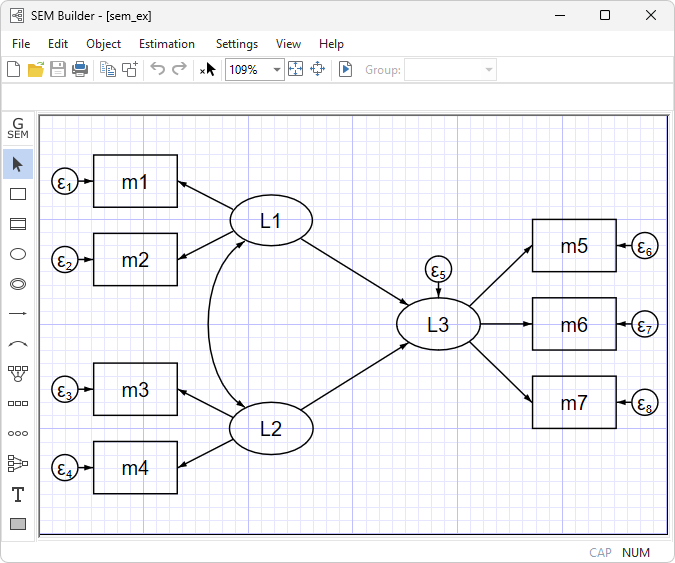
or use the command syntax 

. sem (L1 -> m1 m2)
      (L2 -> m3 m4)
      (L3 <- L1 L2)
      (L3 -> m5 m6 m7)

It’s the same model either way.

Stata’s SEM Builder uses standard path notation.

In command syntax, you type the path diagram. Capitalized names are latent variables. Lowercased names are observed variables. You can type arrows in either direction. The above model could be equally well typed as 

. sem (m1 m2 <- L1)
      (L2 -> m3 m4)
      (L3 <- L1 L2)
      (L3 -> m5 m6 m7)

and order does not matter, and neither does spacing: 

. sem (m1 m2 <- L1) (L2 -> m3 m4) (L3 -> m5 m6 m7) (L3 <- L1 L2)

You can specify paths individually, 

. sem (m1 <- L1) (m2 <- L1) (L2 -> m3) (L2 -> m4)  (L3 -> m5) (L3 -> m6) (L3 -> m7) (L3 <- L1) (L3 <- L2)

or combined, 

. sem (m1 m2 <- L1) (L2 -> m3 m4) (L3 -> m5 m6 m7) (L3 <- L1 L2)

Let's see it work

Let’s fit a structural model with a measurement component using data from Wheaton, Muthén, Alwin, and Summers (1977): 

. webuse sem_sm2, clear
(Structural model with measurement component)

. ssd describe

  Summary statistics data from https://www.stata-press.com/data/r17/sem_sm2.dta
  Observations:             932          Structural model with measurem..
     Variables:              13          25 May 2020 11:45
                                         (_dta has notes)



 


Variable name                  Variable label


 

educ66                         Education, 1966
  occstat66                      Occupational status, 1966
  anomia66                       Anomia, 1966
  pwless66                       Powerlessness, 1966
  socdist66                      Latin American social distance, 1966
  occstat67                      Occupational status, 1967
  anomia67                       Anomia, 1967
  pwless67                       Powerlessness, 1967
  socdist67                      Latin American social distance, 1967
  occstat71                      Occupational status, 1971
  anomia71                       Anomia, 1971
  pwless71                       Powerlessness, 1971
  socdist71                      Latin American social distance, 1971


 

. notes

_dta:
  1.  Summary statistics data from Wheaton, B., Muthen B., Alwin, D., & Summers,
      G., 1977, "Assessing reliability and stability in panel models", in D. R.
      Heise (Ed.), _Sociological Methodology 1977_ (pp. 84-136), San Francisco:
      Jossey-Bass, Inc.
  2.  Four indicators each measured in 1966, 1967, and 1981, plus another indicator
      (educ66) measured only in 1966.
  3.  Intended use: Create structural model relating Alienation in 1971, Alienation
      in 1967, and SES in 1966.

Below we will demonstrate

Show me, fitting the model

Simplified versions of the model fit by the authors of the referenced paper appear in many SEM software manuals. One simplified model is

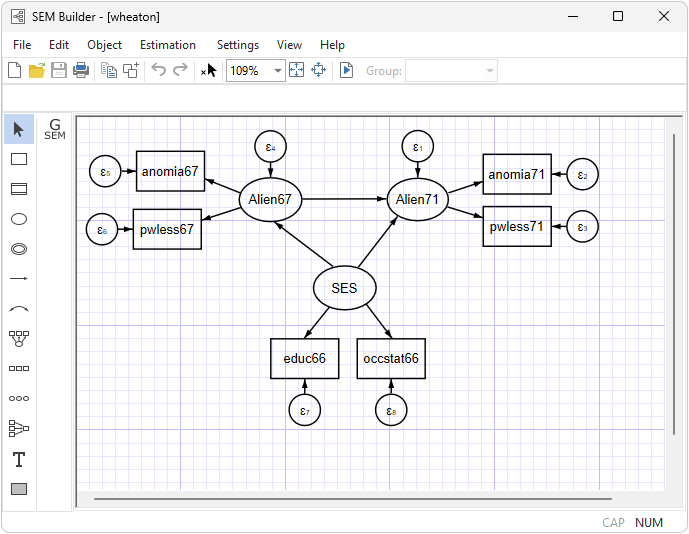
You can also readily fit this model using the following command: 

. sem    
   (anomia67 pwless67 <- Alien67)          /// measurement piece
   (anomia71 pwless71 <- Alien71)          /// measurement piece
   (Alien67 <- SES)                        /// structural piece
   (Alien71 <- Alien67 SES)                /// structural piece
   (    SES -> educ occstat66), nolog      /// measurement piece

And the results are 

Endogenous variables
  Measurement: anomia67 pwless67 anomia71 pwless71 educ66 occstat66
  Latent:      Alien67 Alien71

Exogenous variables
  Latent: SES

Structural equation model                                  Number of obs = 932
Estimation method: ml

Log likelihood = -15246.469

 ( 1)  [anomia67]Alien67 = 1
 ( 2)  [anomia71]Alien71 = 1
 ( 3)  [educ66]SES = 1


 

                                OIM 

                Coefficient  std. err.      z    P>|z|     [95% conf. interval] 

    

Structural       

  Alien67         

           SES    -.6140404   .0562407   -10.92   0.000    -.7242701   -.5038107 

      

  Alien71          

        Alien67     .7046342   .0533512    13.21   0.000     .6000678    .8092007 

            SES    -.1744153   .0542489    -3.22   0.001    -.2807413   -.0680894 

    

Measurement        

  anomia67         

        Alien67            1  (constrained) 

          _cons        13.61   .1126205   120.85   0.000     13.38927    13.83073 

      

  pwless67         

        Alien67     .8884887   .0431565    20.59   0.000     .8039034    .9730739 

          _cons        14.67   .1001798   146.44   0.000     14.47365    14.86635 

      

  anomia71         

        Alien71            1  (constrained) 

          _cons        14.13   .1158943   121.92   0.000     13.90285    14.35715 

      

  pwless71         

        Alien71     .8486022   .0415205    20.44   0.000     .7672235    .9299808 

          _cons         14.9   .1034537   144.03   0.000     14.69723    15.10277 

      

  educ66           

            SES            1  (constrained) 

          _cons         10.9   .1014894   107.40   0.000     10.70108    11.09892 

      

  occstat66        

            SES     5.331259   .4307503    12.38   0.000     4.487004    6.175514 

          _cons        37.49   .6947112    53.96   0.000     36.12839    38.85161 

    

 var(e.anomia67)    4.009921   .3582978                      3.365724    4.777416 

 var(e.pwless67)    3.187468    .283374                      2.677762    3.794197 

 var(e.anomia71)    3.695593   .3911512                      3.003245     4.54755 

 var(e.pwless71)    3.621531   .3037908                      3.072483    4.268693 

   var(e.educ66)    2.943819   .5002527                      2.109908    4.107319 

var(e.occstat66)      260.63   18.24572                      227.2139    298.9605 

  var(e.Alien67)    5.301416    .483144                      4.434225    6.338201 

  var(e.Alien71)    3.737286   .3881546                      3.048951    4.581019 

        var(SES)     6.65587   .6409484                      5.511067    8.038482 


LR test of model vs. saturated: chi2(6) = 71.62              Prob > chi2 = 0.0000

Notes:

  1. Measurement component: In both 1967 and 1971 anomia and powerlessness are used to measure endogenous latent variables representing Alienation for the same two years. Education and occupational status are used to measure the exogenous latent variable SES.

  2. Structural component: SES->Alien67 and SES->Alien71, and Alien67->Alien71.

  3. The model vs. saturated chi-squared test indicates the model is a poor fit.

Show me, modification indices

That the model is a poor fit leads us to looking at the modification indices: 

. estat mindices

Modification indices





                                                                 Standard


                                   MI     df   P>MI        EPC        EPC


   


Measurement                 


  anomia67                  


                 anomia71      51.977      1   0.00   .3906425   .4019984


                 pwless71      32.517      1   0.00  -.2969297  -.2727609


                   educ66       5.627      1   0.02   .0935048   .0842631


     


  pwless67                  


                 anomia71      41.618      1   0.00  -.3106995  -.3594367


                 pwless71      23.622      1   0.00   .2249714   .2323233


                   educ66       6.441      1   0.01  -.0889042  -.0900664


     


  anomia71                  


                 anomia67      58.768      1   0.00    .429437   .4173061


                 pwless67      38.142      1   0.00  -.3873066  -.3347904


     


  pwless71                  


                 anomia67      46.188      1   0.00  -.3308484  -.3601641


                 pwless67      27.760      1   0.00   .2871709   .2780833


     


  educ66                    


                 anomia67       4.415      1   0.04   .1055965   .1171781


                 pwless67       6.816      1   0.01  -.1469371  -.1450411


   


cov(e.anomia67,e.anomia71)     63.786      1   0.00   1.951578   .5069627


cov(e.anomia67,e.pwless71)     49.892      1   0.00  -1.506704  -.3953794


  cov(e.anomia67,e.educ66)      6.063      1   0.01   .5527612   .1608845


cov(e.pwless67,e.anomia71)     49.876      1   0.00  -1.534199  -.4470094


cov(e.pwless67,e.pwless71)     37.357      1   0.00   1.159123    .341162


  cov(e.pwless67,e.educ66)      7.752      1   0.01  -.5557802  -.1814365




EPC is expected parameter change.

Notes:

  1. There are lots of statistically significant paths we could add to the model.

  2. Some of those statistically significant paths also make theoretical sense.

  3. Two in particular that make sense are the covariances between e.anomia67 and e.anomia71, and between e.pwless67 and e.pwless71.

Show me, refitting the model

Let’s refit the model and include those two previously excluded covariances: 

. sem                        
   (anomia67 pwless67 <- Alien67)          /// measurement piece
   (anomia71 pwless71 <- Alien71)          /// measurement piece
   (Alien67 <- SES)                        /// structural piece
   (Alien71 <- Alien67 SES)                /// structural piece
   (    SES -> educ occstat66)             /// measurement piece
          , cov(e.anomia67*e.anomia71)       
          cov(e.pwless67*e.pwless71) nolog

And the results are 

Endogenous variables
  Measurement: anomia67 pwless67 anomia71 pwless71 educ66 occstat66
  Latent:      Alien67 Alien71

Exogenous variables
  Latent: SES

Structural equation model                                  Number of obs = 932
Estimation method: ml

Log likelihood = -15213.046

 ( 1)  [anomia67]Alien67 = 1
 ( 2)  [anomia71]Alien71 = 1
 ( 3)  [educ66]SES = 1





                                OIM


                Coefficient  std. err.      z    P>|z|     [95% conf. interval]


   


Structural      


  Alien67       


          SES    -.5752228    .057961    -9.92   0.000    -.6888244   -.4616213


     


  Alien71       


      Alien67      .606954   .0512305    11.85   0.000     .5065439     .707364


          SES    -.2270301   .0530773    -4.28   0.000    -.3310596   -.1230006


   


Measurement     


  anomia67      


      Alien67            1  (constrained)


        _cons        13.61   .1126143   120.85   0.000     13.38928    13.83072


     


  pwless67      


      Alien67     .9785952   .0619825    15.79   0.000     .8571117    1.100079


        _cons        14.67   .1001814   146.43   0.000     14.47365    14.86635


     


  anomia71      


      Alien71            1  (constrained)


        _cons        14.13   .1159036   121.91   0.000     13.90283    14.35717


     


  pwless71      


      Alien71     .9217508   .0597225    15.43   0.000     .8046968    1.038805


        _cons         14.9   .1034517   144.03   0.000     14.69724    15.10276


     


  educ66        


          SES            1  (constrained)


        _cons         10.9   .1014894   107.40   0.000     10.70108    11.09892


     


  occstat66     


          SES      5.22132    .425595    12.27   0.000     4.387169    6.055471


        _cons        37.49   .6947112    53.96   0.000     36.12839    38.85161


   


var(e.anom~67)    4.728874    .456299                      3.914024    5.713365


var(e.pwle~67)    2.563413   .4060733                      1.879225      3.4967


var(e.anom~71)    4.396081   .5171156                      3.490904    5.535966


var(e.pwle~71)    3.072085   .4360333                      2.326049    4.057398


 var(e.educ66)    2.803674   .5115854                      1.960691    4.009091


var(e.occs~66)    264.5311   18.22483                      231.1177    302.7751


var(e.Alien67)    4.842059   .4622537                      4.015771    5.838364


var(e.Alien71)    4.084249   .4038995                      3.364613    4.957802


      var(SES)    6.796014   .6524866                      5.630283    8.203105


   


cov(e.anom~67,  


   e.anomia71)    1.622024   .3154267     5.14   0.000     1.003799    2.240249


cov(e.pwle~67,  


   e.pwless71)    .3399961   .2627541     1.29   0.196    -.1749925    .8549847




LR test of model vs. saturated: chi2(4) = 4.78             Prob > chi2 = 0.3111

Notes:

  1. We find the covariance between e.anomia67 and e.anomia71 to be significant(Z=5.14).

  2. We find the covariance between e.pwless67 and e.pwless71 to be insignificant at the 5% level (Z=1.29).

Products

New in Stata 18

Why Stata

All features

Disciplines

Stata/MP

Order Stata

Purchase

Order Stata

Bookstore

Stata Press

Stata Journal

Gift Shop

Learn

NetCourses

Classroom and web training

Organizational training

Webinars

Video tutorials

Third-party courses

Web resources

Teaching with Stata

Support

Training

Video tutorials

FAQs

Statalist: The Stata Forum

Resources

Technical support

Customer service

Company

Contact us

News and events

Customer service

Careers

Search

© Copyright 1996–2024 StataCorp LLC. All rights reserved.

Terms of use | Privacy policy | Contact us