New in SEM (structural equation modeling)
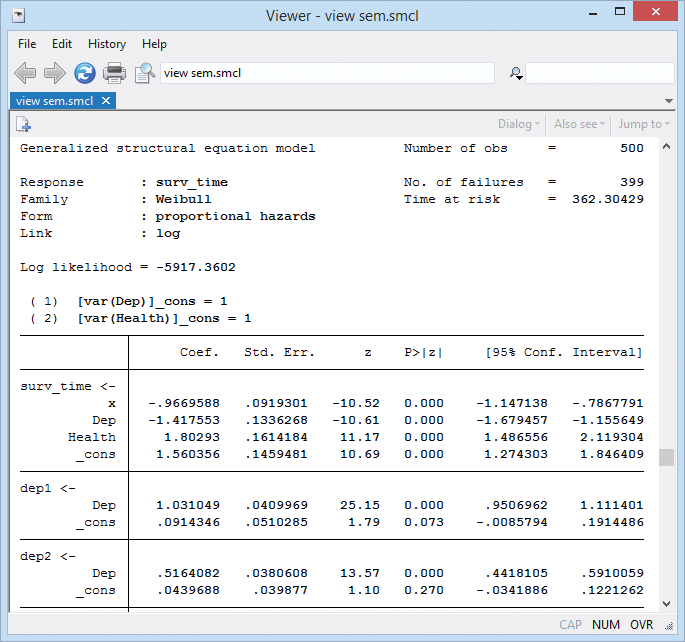
- Survival models (parametric)
- Latent predictors
- Mediation models and more
- Unobserved components
- Multilevel survival models—random intercepts and random coefficients
- Survival outcomes with other outcomes
- Right-censoring
- Left-truncation
- Exponential, loglogistic, Weibull, lognormal, and gamma survival distributions
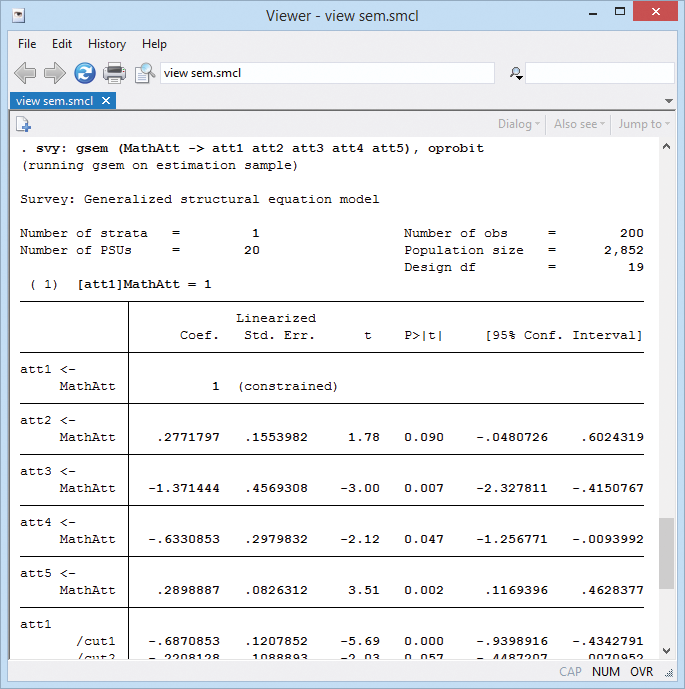
- Generalized models now support survey data
- Adjusted point estimates, SEs, and tests
- Observation-level sampling weights
- Sampling weights at each stage of survey (multilevel models)
- Clustered sampling
- Stratified sampling and poststratification
- Finite population corrections
- Linearized, bootstrap, jackknife, or BRR standard errors
- Satorra–Bentler scaled Χ2
- Adjustment for nonnormal data
- All relevant goodness-of-fit statistics adjusted
- Robust standard errors and postestimation tests
SEM handles one or more latent (unobserved) variables.
(They can be exogenous or endogenous.)
SEM handles one or more observed endogenous variables (and the structural relationships among them).
SEM handles multilevel random effects and random coefficients.
SEMs can be linear or generalized linear, meaning probit, logit, Poisson, and others.
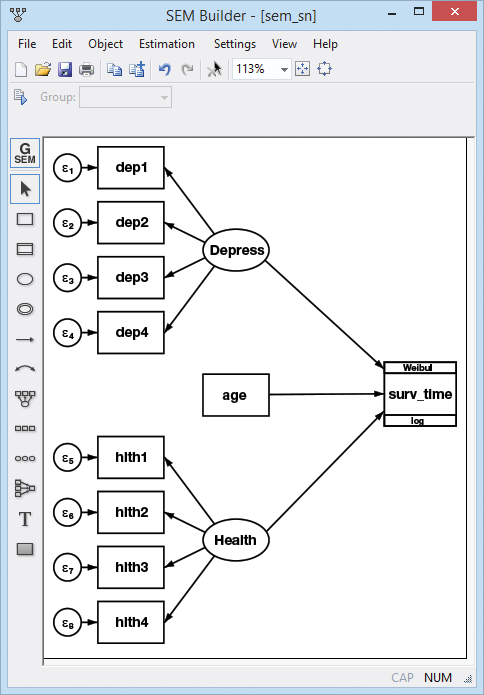
Example 1: Survival model
Let's do a survival model combined with CFA (confirmatory factor analysis). CFAs model the level of a latent trait using observable measurements.
We analyze survival times of nursing home residents. We have censored data; thankfully, not all the residents have died yet.
- We posit that survival times are determined by age, depression level, and overall health.
- We have four variables that each measure aspects of depression (our first latent trait).
- We have four variables that each measure aspects of health (our second latent trait).