You can use Mata interactively.
A = 1,2\3,4 // Input a 2 × 2 matrix
b = -1\3 // Input a 2 × 1 column vector
A'b // Compute A'b
A[2,1] // Access the (2,1) element of A
A[,2] // Access the second column of A
B = diag(b) // Create a 2 × 2 matrix with the elements of b on the diagonal
C = A,B // Combine matrices A and B by column
D = A\B // Or by row
I = I(3) // Create a 3 × 3 identity matrix I
trace(A) // Compute the trace of A
det(A) // And the determinant of A
G*H // Multiply G (n × k) by H (k × k)
G:*g // Multiply each column of G (n × k) by g (n × 1)
st_data(.,.) // Load Stata dataset into Mata
st_data((1,5\7,9), "mpg") // Observations 1 to 5 and 7 to 9 of variable mpg
Or you can write a simple program for regression.
mata
st_view(y=., ., "mpg")
st_view(X=., ., ("weight", "foreign", "cons"))
b = invsym(X'X)*X'y
b
e = y - X*b
n = rows(X)
k = cols(X)
s2= (e'e)/(n-k)
V = s2*invsym(X'X)
V
se = sqrt(diagonal(V))
(b, se)
Or build a regression system using structures or classes.
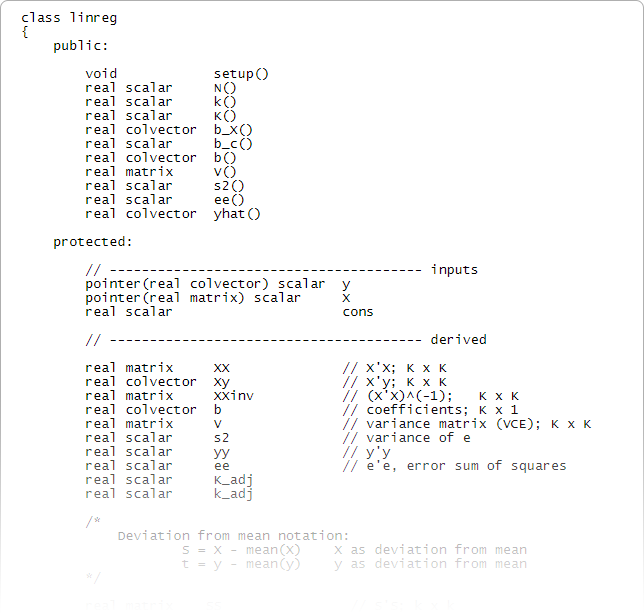
class linreg
{
public:
void setup()
real scalar N()
real scalar k()
real scalar K()
real colvector b_X()
real scalar b_c()
real colvector b()
real matrix V()
real scalar s2()
real scalar ee()
real colvector yhat()
protected:
// --------------------------------------- inputs
pointer(real colvector) scalar y
pointer(real matrix) scalar X
real scalar cons
// --------------------------------------- derived
real matrix XX // X'X; K x K
real colvector Xy // X'y; K x K
real matrix XXinv // (X'X)^(-1); K x K
real colvector b // coefficients; K x 1
real matrix V // variance matrix (VCE); K x K
real scalar s2 // variance of e
real scalar yy // y'y
real scalar ee // e'e, error sum of squares
real scalar K_adj
real scalar k_adj
/*
Deviation from mean notation:
S = X - mean(X) X as deviation from mean
t = y - mean(y) y as deviation from mean
*/
real matrix SS // S'S; k x k
real colvector St // S't; K x 1 (sic)
real matrix SSinv // (S'S)^(-1); K x K (sic)
real rowvector mean_X // means of rows of X; 1 x k
real scalar mean_y // mean of row of y; 1 x 1
void init()
real matrix XX()
real colvector Xy()
real scalar yy()
real matrix XXinv()
real matrix SSinv()
void calc_SSinv_cons()
real matrix SS()
real colvector St()
real rowvector mean_X()
real scalar mean_y()
real scalar K_adj()
real scalar k_adj()
}
void linreg::init()
{
XX = .z
Xy = .z
XXinv = .z
b = .z
V = .z
s2 = .z
yy = .z
ee = .z
SS = .z
St = .z
mean_X = .z
mean_y = .z
SSinv = .z
K_adj = .z
k_adj = .z
}
/* -------------------------------------------------- entry points --- */
void linreg::setup( real colvector user_y,
real matrix user_X,
real scalar user_cons )
{
assert(rows(y)==rows(X))
y = &user_y
X = &user_X
cons = (user_cons!=0)
init() // initialize derived vars
}
real scalar linreg::N() return(rows(*X))
real scalar linreg::k() return(cols(*X))
real scalar linreg::K() return(cols(*X) + cons)
/*
Throughout this code, distinguish between k and K:
k = # of independent variables EXCLUDING intercept
K = # of independent variables INCLUDING intercept
In models without an intercept, K = k
In models with an intercept, K = k + 1
Note: *X is k x k, X does not include vector of 1s, and
b is K x 1, coefficient include intercept if there is one.
To code the equivalent of X*b, you extract the first k elements
of b and add the intercept separately. To make this easier
think of
b = (b_X, b_c)
b_X() returns b_X: 1 x k
b_c() returns b_c: 1 x 1 containing b[K] or 0.
Thus, X*b can be calculated as (*X)*b_X() :+ b_c()
in all cases.
*/
real colvector linreg::b_X()
{
if (cons) {
if (k()) return( b()[| 1\k() |])
else return( J(0, 1, .))
}
else return(b())
}
real scalar linreg::b_c()
{
return(cons ? b()[K()] : 0)
}
real colvector linreg::b()
{
if (b == .z) {
if (cons) {
b = SSinv() * St()
b[K()] = mean_y() - mean_X()*b_X()
}
else b = XXinv() * Xy()
}
return(b)
}
real matrix linreg::V()
{
if (V == .z) {
V = s2() * (cons ? SSinv() : XXinv())
}
return(V)
}
real scalar linreg::s2()
{
if (s2 == .z) {
s2 = ee() / ( N() - K_adj() )
}
return(s2)
}
real scalar linreg::ee()
{
real colvector e
if (ee == .z) {
e = *y - yhat()
ee = quadcross(e, e)
}
return(ee)
}
real colvector linreg::yhat()
{
return( (*X)*b_X() :+ b_c() )
}
/* ------------------------------------------internal subroutines --- */
real matrix linreg::XX()
{
if (XX == .z) {
XX = quadcross(*X, cons, *X, cons)
}
return(XX)
}
real colvector linreg::Xy()
{
if (Xy == .z) {
Xy = quadcross(*X, cons, *y, 0)
}
return(Xy)
}
real scalar linreg::yy()
{
if (yy == .z) {
yy = quadcross(*y, *y)
}
return(yy)
}
real matrix linreg::XXinv()
{
if (XXinv == .z) {
XXinv = invsym(XX())
}
return(XXinv)
}
real matrix linreg::SSinv()
{
if (SSinv == .z) {
if (cons) calc_SSinv_cons()
}
return(SSinv)
}
void linreg::calc_SSinv_cons()
{
real scalar K, k, i
real rowvector v
real matrix kxk, rowK, colK
K = K() // # X vars including constant
k = k() // # x vars excluding constant
/*
Calculate inverse of S'S = SS().
This routine called only if cons, meaning K = k + 1.
SS() is k x k -- it excludes constant.
We want the full K x K inverse.
*/
// ---------------------------------------- SSinv 1 x 1 case ---
if (K==1) {
SSinv = 1/N()
return
}
// ----------------------------------- SSinv 2 x 2 or larger ---
SSinv = J(K, K, .) // matrix now K x K
// Range subscripts:
kxk = (1,1 \ k,k) // k x k submatrix rows & cols 1..k
rowK = (K,1 \ K,k) // 1 x k submatrix; row K
colK = (1,K \ k,K) // k x 1 submatrix; col K
SSinv[|kxk |] = invsym(SS())
SSinv[|rowK|] = v = -(mean_X() * SSinv[|kxk|])
SSinv[|colK|] = v'
// SSinv[ K,K ] = 1/N() - mean_X()*SSinv[|colK|]
SSinv[ K,K ] = 1/N() - mean_X()*v'
}
real matrix linreg::SS()
{
if (SS == .z) {
if (cons) {
SS = quadcrossdev(*X, 0, mean_X(),
*X, 0, mean_X() )
}
}
return(SS)
}
real colvector linreg::St()
{
if (St == .z) {
St = quadcrossdev(*X, 0, mean_X(),
*y, 0, mean_y()) \ 0
}
return(St)
}
real rowvector linreg::mean_X()
{
if (mean_X == .z) mean_X = mean(*X)
return(mean_X)
}
real scalar linreg::mean_y()
{
if (mean_y == .z) mean_y = mean(*y)
return(mean_y)
}
real scalar linreg::K_adj()
{
if (K_adj == .z) {
if (cons) K_adj = colsum(diagonal(SSinv()) :!= 0)
else K_adj = colsum(diagonal(XXinv()) :!= 0)
}
return(K_adj)
}
real scalar linreg::k_adj()
{
if (k_adj == .z) {
k_adj = k() - (K()-K_adj())
}
return(k_adj)
}
end
Resources
There are many great resources for learning Mata.
The official documentation:
We recommend starting with the intro sections:
The Mata Book: A Book for Serious
Programmers and Those Who Want to Be by William Gould
The Mata Matters articles published in the Stata Journal:
Programming an estimation command in Stata, a series of posts on the Stata Blog.
An Introduction to Mata
from the Social Science Computing Cooperative at the University of Madison–Wisconsin
Estimation of the Mixture of Gaussians Using Mata, blog post by Aramayis Dallakyan.
Learn more about all of Mata's features.
