
Marginal analysis was introduced in Stata 11.
|
| Order |
Stata 11 does margins. Does estimated marginal means. Does least-squares means. Does average and conditional marginal/partial effects, as derivatives or elasticities. Does average and conditional adjusted predictions. Does predictive margins. Does more. Margins are statistics calculated from predictions of a previously fit model at fixed values of some covariates and averaging or otherwise integrating over the remaining covariates.
If that sounds overly technical, try this. margins answers the question, “What does my model have to say about such-and-such a group or such-and-such a person”, where such-and-such might be:
It answers these questions either conditionally—based on fixed values of covariates—or averaged over the observations in a sample. Any sample.
It answers these questions about any prediction or any other response you can calculate as a function of your estimated parameters—linear responses, probabilities, hazards, survival times, odds ratios, risk differences, etc.
It answers these questions in terms of the response given covariate levels, or in terms of the change in the response for a change in levels, a.k.a. marginal effects.
It answers these questions providing standard errors, test statistics, and confidence intervals and those statistics can take the covariates as given or adjust for sampling, a.k.a predictive margins and survey statistics.
Say that we are interested in the outcome y based on a person’s gender and packages of cigarettes smoked per day. Using Stata’s new factor-variable notation, we can fit a logistic regression by typing
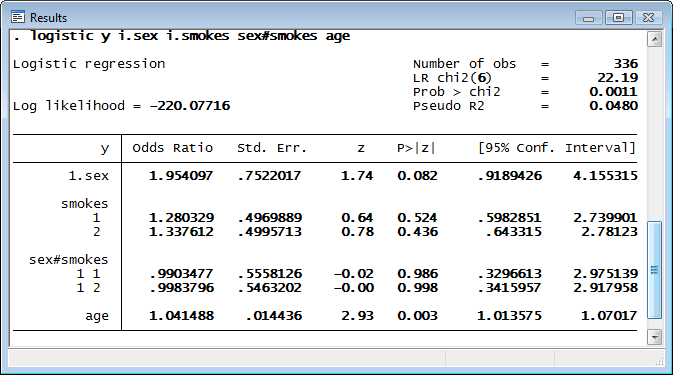
The interaction between sex and smokes makes interpretation difficult. We can use margins to decipher their effects:
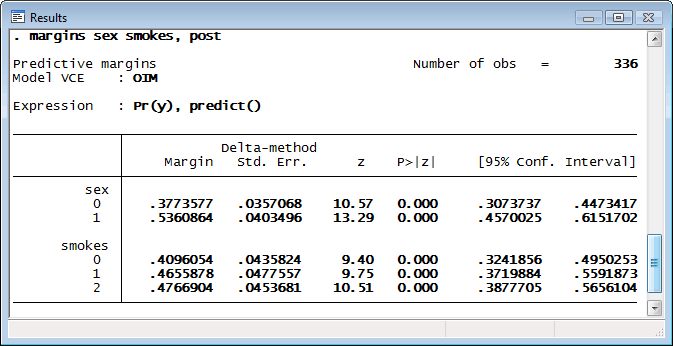
We obtain predictive margins. If the distribution of the cigarettes smoked remains the same in the population, but everyone were male, we would expect about 38% to have a positive outcome for y. If everyone were female; 54%. If instead the distribution of males and females were as observed but no one smoked, we would expect about 41% to have a positive outcome.
Is there a significant difference in the probability of a positive outcome between males and females? We can run tests after margins to find out:
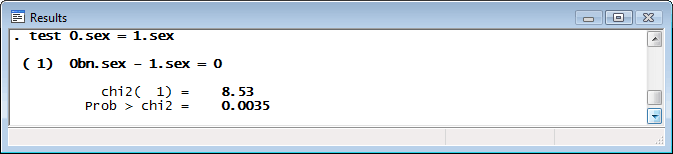
We find evidence that the predicted margins for males and females differ.
Let's see an example of marginal effects. Because of Stata 11’s new factor-variable features, we can get average partial and marginal effects for age even when age enters as a polynomial:
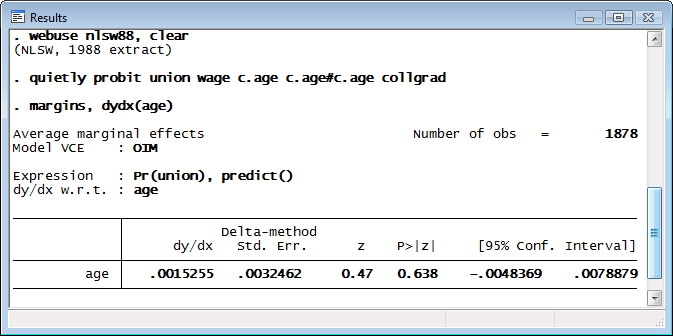
We are using different data than before. The probability that a person is in a union increases by 0.0015 as age increases by one year. By default, margins reports average marginal (partial) effects, which means effects are calculated for each observation in the data and then averaged.
Alternatively, if we wanted effects at the average of the covariates, we could type
. margins, dydx(age) atmeans
Stata 11’s margins command includes options to control whether the standard errors reflect just the sampling variation of the estimated coefficients or whether they also reflect the sampling variation of the estimation sample. In the latter case, margins can account for complex survey sampling including weights, sampling units, pre- and poststratification, and subpopulations.
margins works after EVERY Stata estimation command except exact logistic and exact Poisson; alternative-specific conditional logistic, alternative-specific multinomial probit, and alternative-specific rank-ordered probit; nested logit; generalized method of moments; and structural vector autoregressive models.