Multilevel survival models
- Parametric survival models with multiple levels of random effects
- Random intercepts and random coefficients
- Crossed random effects
- Right-censoring
- Single- and multiple-record survival-time data
- Normal random effects rather than often less plausible gamma frailties
- Fits exponential, loglogistic, Weibull, lognormal, and gamma survival models
- Graphs of marginal survivor, cumulative hazard, and hazard functions
- Fully integrated with Stata's st and me
We model the effects of laparoscopic surgery and age on length of hospital stay (LOS) for adult patients with appendicitis. We believe that doctors affect the length of a patient's stay, so we include a random effect for doctor. We further believe that hospitals vary in their discharge procedures and thus also affect LOS, so we include a random effect for hospital. We will assume that hospitals nest doctors nest patients.
We will model LOS using survival-time analysis. We first stset our survival data by typing stset los.
In these data, we observe the LOS for all patients; there is no censoring. Rather oddly but not uncommonly, the "failure" is the happy event of departing the hospital.
We will fit a Weibull model for length of stay:
. mestreg lap_surg age || hospital: || doctor:, distribution(weibull)
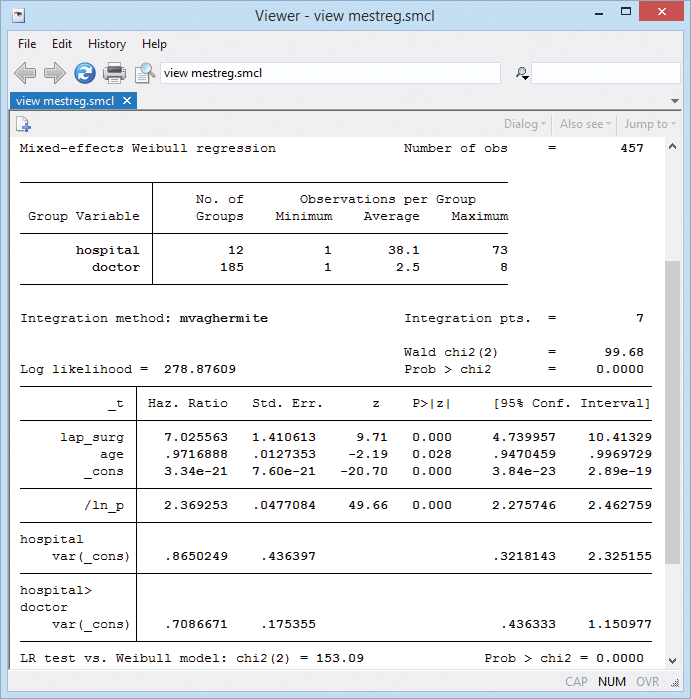
Stata will report the results in either the accelerated failure-time or the proportional-hazards metric. These results are in the hazard metric. Laparoscopic surgery has a hazard ratio > 1 and so decreases LOS. Age has a hazard ratio < 1 and so increases LOS.
Far more importantly, we see a large variation across both doctor and hospital that might have contaminated our results had we not taken them into account.
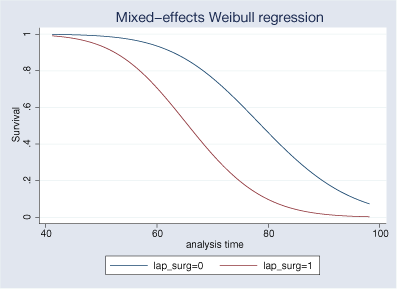
We can plot the marginal survivor function for surgery method:
. stcurve, survival at1(lap_surg=0) at2(lap_surg=1)
 Upgrade now
Order Stata
Upgrade now
Order Stata Read even more about multilevel survival models.







