
$$ \begin{align} y &= X \beta + \sum_{k}^{K} W_{k} X \gamma_{k} + \sum_{p=1}^{P} \lambda_p W_{p} y + u \nonumber \\ u &= \sum_{q=1}^Q \rho_q M_{q} u + \epsilon \end{align} $$
| Repeatable | ||||
|---|---|---|---|---|
| Math term | Spillover | Stata option | GS2SLS | ML |
| $\sum_{k}^{K} W_{k} X \gamma_{k} $ | Local spillover | ivarlag() | $\checkmark$ | $\checkmark$ |
| $\sum_{p=1}^{P} \lambda_p W_{p} y$ | Global spillover in outcome | dvarlag() | $\checkmark$ | $\color{red}\times$ |
| $\sum_{q=1}^Q \rho_q M_{q} u$ | Global spillover in unobserved errors | errorlag() | $\checkmark$ | $\color{red}\times$ |
| estimator | higher order SARAR(p,q) | non-normal errors | heteroskedastic errors | efficiency in i.i.d | Computation time |
|---|---|---|---|---|---|
| ml | $\color{red}\times$ | $\checkmark$ | $\color{red}\times$ | more | Not very fast |
| GSLSLS | $\checkmark$ | $\checkmark$ | $\checkmark$ | less | fast |
|
|

|
|
$$ \begin{align*} y = X \beta + \lambda W y + \epsilon \\ \end{align*} $$
$$ \Delta x_i \rightarrow y_i \rightarrow \text{neighbor of $y_i$} \rightarrow \text{neighbors of neighbors of $y_i$} \rightarrow \ldots \rightarrow \text{all of y} $$
$$ \Delta e_i \rightarrow y_i \rightarrow \text{neighbor of $y_i$} \rightarrow \text{neighbors of neighbors of $y_i$} \rightarrow \ldots \rightarrow \text{all of y} $$
$$ \begin{align*} y = X \beta + u \\ u = \rho M u + \epsilon \end{align*} $$
$$ \Delta x_i \rightarrow y_i \text{ (END) } $$
$$ \Delta e_i \rightarrow u_i \rightarrow \text{neighbor of $u_i$} \rightarrow \text{neighbors of neighbors of $u_i$} \rightarrow \ldots \rightarrow \text{all of $y$} $$
| shock $x_i$ | shock $e_i$ | |
|---|---|---|
| spatial lag |
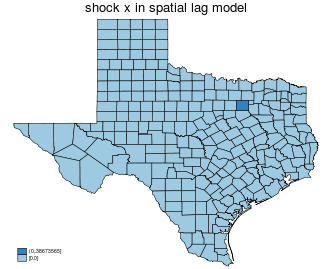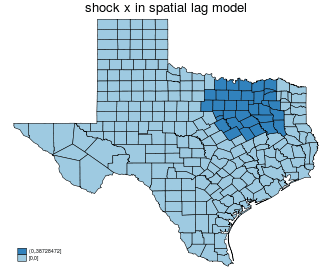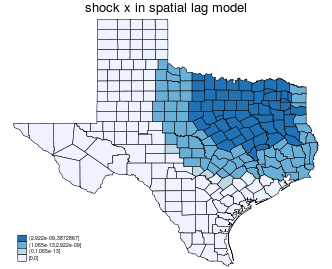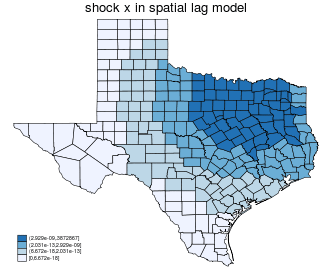
|
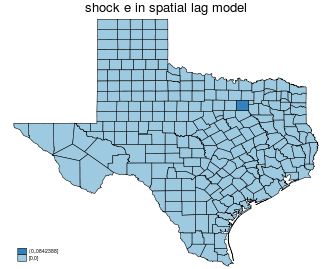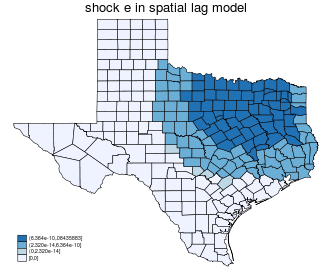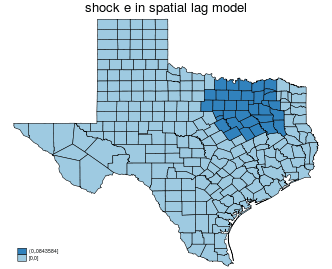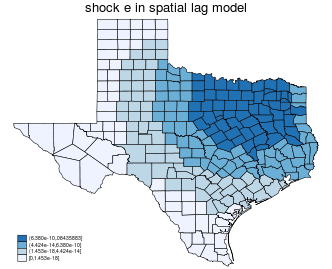
|
| spatial error |
|
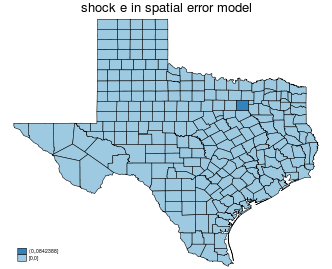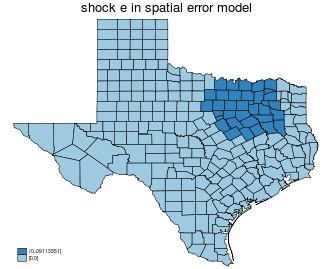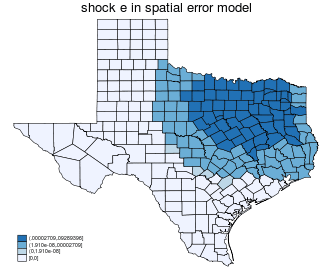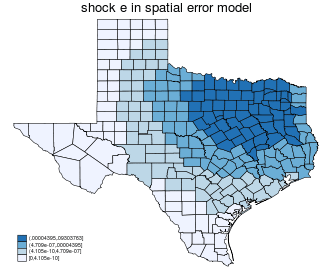
|
. use texas, clear
(S.Messner et al.(2000), U.S southern county homicide rates in 1990)
. spmatrix create contiguity W, replace
. // spatial lag model
. qui spregress hrate gini, dvarlag(W) gs2sls
. estat impact
progress :100%
Average impacts Number of obs = 254
------------------------------------------------------------------------------
| Delta-Method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
direct |
gini | 46.40452 14.15254 3.28 0.001 18.66605 74.14299
-------------+----------------------------------------------------------------
indirect |
gini | .0432249 8.762717 0.00 0.996 -17.13138 17.21783
-------------+----------------------------------------------------------------
total |
gini | 46.44774 15.25232 3.05 0.002 16.55375 76.34174
------------------------------------------------------------------------------
. // spatial error model
. qui spregress hrate gini, errorlag(W) gs2sls
. estat impact
progress :100%
Average impacts Number of obs = 254
------------------------------------------------------------------------------
| Delta-Method
| dy/dx Std. Err. z P>|z| [95% Conf. Interval]
-------------+----------------------------------------------------------------
direct |
gini | 47.41769 14.79948 3.20 0.001 18.41124 76.42413
-------------+----------------------------------------------------------------
indirect |
gini | 0 (omitted)
-------------+----------------------------------------------------------------
total |
gini | 47.41769 14.79948 3.20 0.001 18.41124 76.42413
------------------------------------------------------------------------------
Divide each entries $w_{i,j}$ by a unique scalar $c$. where the scalar $c$ can be largest eigenvalues, the minimum of the maximum of rowsum and colsum. $$ W_{i,j}^{*} = \frac{W_{i,j}^{(o)}}{c} $$
Divide each entries $w_{i,j}$ by its row sum. $$ W_{i,j}^{*} = \frac{W_{i,j}^{(o)}}{\sum_{i=1}^n{W_{i,j}^{(o)}}} $$
. // norm(none)
. spmatrix create contiguity W_o in 1/5, replace norm(none)
. spmatrix matafromsp W_o id = W_o
. // norm(spectral)
. spmatrix create contiguity W_spec in 1/5, replace norm(spectral)
. spmatrix matafromsp W_spec id = W_spec
. // norm(minmax)
. spmatrix create contiguity W_minmax in 1/5, replace norm(minmax)
. spmatrix matafromsp W_minmax id = W_minmax
. // norm(row)
. spmatrix create contiguity W_row in 1/5, replace norm(row)
. spmatrix matafromsp W_row id = W_row
. // display different Ws
. mata :
------------------------------------------------- mata (type end to exit) -----
: W_o
[symmetric]
1 2 3 4 5
+---------------------+
1 | 0 |
2 | 0 0 |
3 | 0 1 0 |
4 | 0 1 0 0 |
5 | 1 0 0 1 0 |
+---------------------+
: W_spec
[symmetric]
1 2 3 4 5
+-----------------------------------------------------------------------+
1 | 0 |
2 | 0 0 |
3 | 0 .5773502692 0 |
4 | 0 .5773502692 0 0 |
5 | .5773502692 0 0 .5773502692 0 |
+-----------------------------------------------------------------------+
: W_minmax
[symmetric]
1 2 3 4 5
+--------------------------+
1 | 0 |
2 | 0 0 |
3 | 0 .5 0 |
4 | 0 .5 0 0 |
5 | .5 0 0 .5 0 |
+--------------------------+
: W_row
1 2 3 4 5
+--------------------------+
1 | 0 0 0 0 1 |
2 | 0 0 .5 .5 0 |
3 | 0 1 0 0 0 |
4 | 0 .5 0 0 .5 |
5 | .5 0 0 .5 0 |
+--------------------------+
: end
-------------------------------------------------------------------------------
. // norm(none)
. spmatrix create contiguity W_o , replace norm(none)
. spregress hrate gini, dvarlag(W_o) ml
. estat impact
. mat b_none = r(b)
. // norm(spectral)
. spmatrix create contiguity W_spec , replace norm(spectral)
. spregress hrate gini, dvarlag(W_spec) ml
. estat impact
. mat b_spec = r(b)
. // norm(minmax)
. spmatrix create contiguity W_minmax , replace norm(minmax)
. spregress hrate gini, dvarlag(W_minmax) ml
. estat impact
. mat b_minmax = r(b)
. // norm(row)
. spmatrix create contiguity W_row , replace norm(row)
. spregress hrate gini, dvarlag(W_row) ml
. estat impact
. // display estat impact
. mat b_row = r(b)
. matrix b = (b_none \ b_spec \ b_minmax \ b_row)
. matrix rownames b = none spec minmax row
. _matrix_table b
----------------------------------------------
| direct indirect total
| gini gini gini
-------------+--------------------------------
none | 44.90757 6.032659 50.94023
spec | 44.90757 6.032664 50.94023
minmax | 44.90757 6.032663 50.94023
row | 43.47706 8.27626 51.75332
----------------------------------------------